infinite pipe

index.html

@@ -0,0 +1 @@
+nafems4.html

nafems4.md

@@ -585,9 +585,8 @@ $$
 
 
 ::::: {#fig:cube}
-![Case B, pure-shear loads](cube-shear.png){#fig:cube-shear width=50%}
-
-![Case C, normal plus shear loads](cube-full.png){#fig:cube-full width=50%}
+![Case B, pure-shear loads](cube-shear.png){#fig:cube-shear width=48%}
+![Case C, normal plus shear loads](cube-full.png){#fig:cube-full width=48%}
 
 Spatial distribution of principal stress\ 3 for cases\ B and\ C. If linearity applied, case\ C would be equal to case\ B plus an constant.
 :::::
@@ -653,27 +652,33 @@ then the sums of their eigenvalues are equal to the eigenvalues of the sums. In
 
 # The infinite pipe revisited after college
 
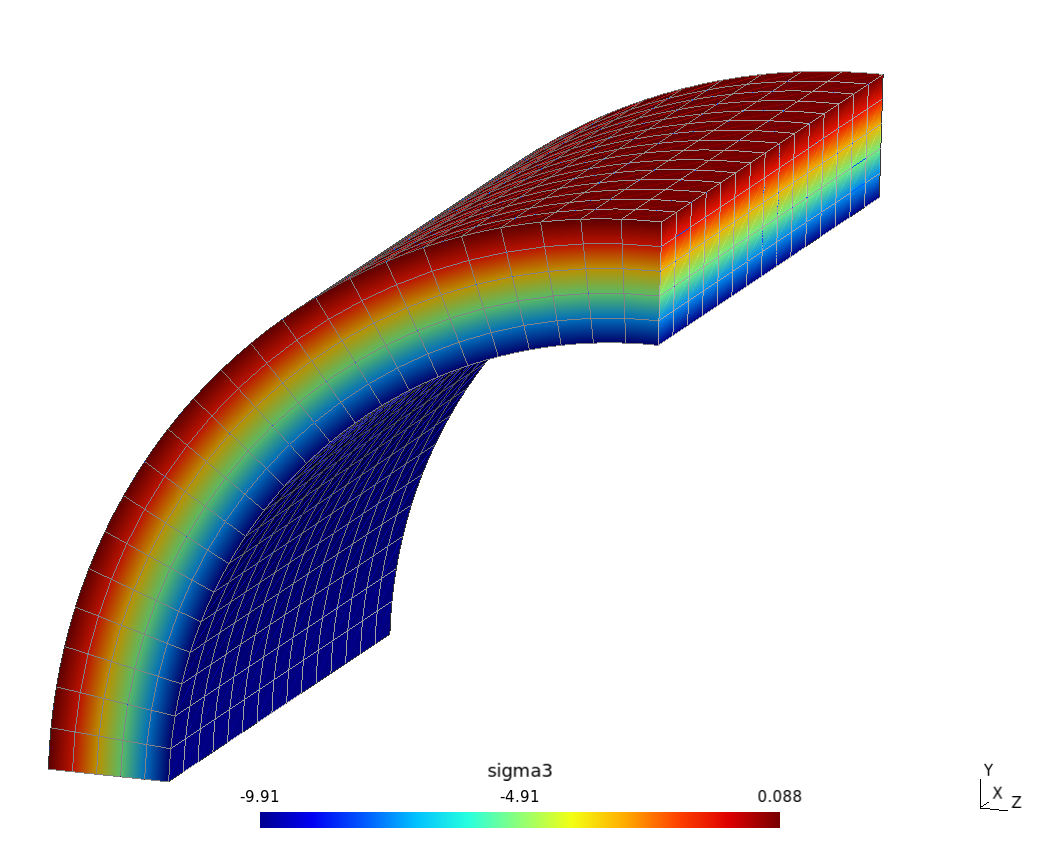
-3D full
-
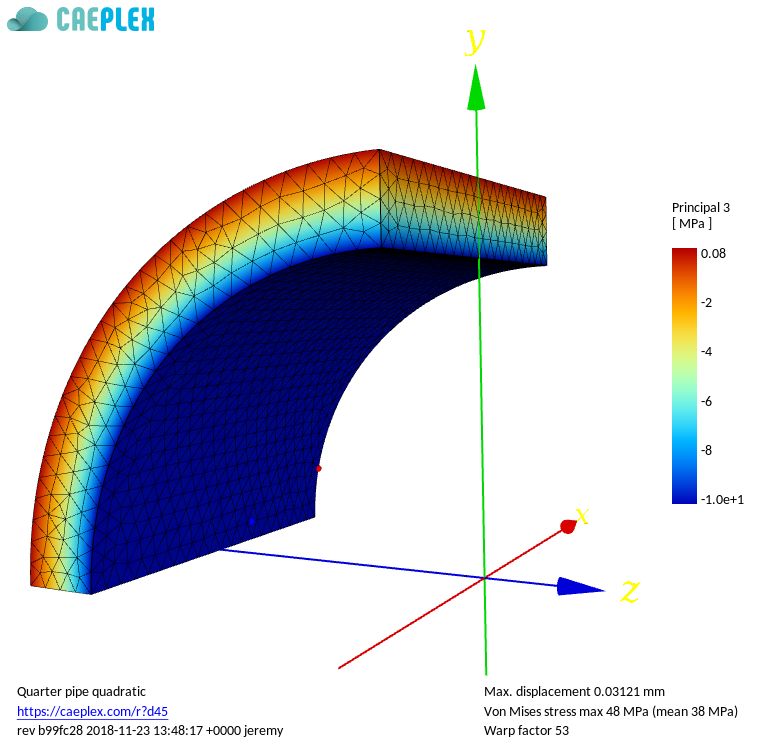
-Quarter
-
-2 grados
-
-2D axysimmetric
+Let us now make a (tiny) step from the general and almost philosophical subject from the last section down to the particular case, and reconsider the infinite pressurized pipe once again. It is time to solve the problem with a computer using finite elements and obtain some funny colored pictures instead of just equations.
 
-1D collocation
+The first thing that has to be said is that, as with any interesting problem, there are literally hundreds or different ways of solving it, each of them throwing particular conclusions. For example, one can:
 
+ 1. solve a real 3D problem or a 2D axisymmetric case (or even a 1D case using the collocation method to solve the radial dependence),
+ 2. have a full cylindrical geometry or just a half (180º), or a quarter (90º), or a thin slice (a small amount of degrees),
+ 3. use a structured or an unstructured grid,
+ 4. uniformly or locally-refine the mesh (with several choices of refinement),
+ 5. use first or second-order (or higher) elements,
+ 6. use tetrahedra or hexahedra,
+ 7. in the case of second-order hexahedra, use complete (i.e. 27-node hexahedron) or incomplete (i.e. 20-node hexahedron) elements,
+ 8. have different mesh refinements from very coarse to very fine,
+ 9. solve the same problem in a few different solvers,
+ 10. etc.
 
-struct vs unstruct
+::::: {#fig:quarter}
+![Quarter-symmetry structured second-order incomplete hexahedra](quarter-struct.png){#fig:cube-struct width=48%}
+![Quarter-symmetry unstructured second-order tetrahedra](quarter-caeplex.png){#fig:quarter-caeplex width=48%}
 
-1st vs 2nd
-
-complete vs incomplete (hexa)
+Two of the hundreds of different ways the infinite pressurized pipe can be solved using FEM.
+:::::
 
 
+You can get both the exponential nature of each added bullet and how easily we can add new further choices to solve a FEM problem. And each of these choices will reveal you something about the nature of either the mechanical problem or the numerical solution. It is not possible to teach any possible lesson from every outcome in college, so you will have to learn them by yourself getting hands at them. I have already tried to address the particular case of the infinite pipe in a [recent report](https://www.seamplex.com/fino/doc/pipe-linearized/) that is worth reading before carrying on with this article.
 
 
-### ASME stress linearization (not linearity!)
+## ASME stress linearization (not linearity!)
 
 
 
@@ -683,8 +688,6 @@ complete vs incomplete (hexa)
 open source!
 que hacen los programas? NADIE SABE
 
-### Young and Poisson
-
 two cubes
 
 ## A parametric tee

simple.html

@@ -99,13 +99,11 @@ $if(title)$
     $endfor$
     $if(date)$
     <p class="lead">$date$
-    $if(rev)$&mdash;$rev$$endif$
-    $if(hash)$&mdash;$hash$$endif$
+    $if(rev)$&mdash;rev.&nbsp;$rev$$endif$
+    $if(hash)$&mdash;<code>$hash$</code>$endif$
     </p>
     $endif$
-    $if(docnumber)$
-    <p class="lead"><a href="$docnumber$.pdf" target="_blank">PDF version</a></p>
-    $endif$
+    <p class="lead"><a href="nafems4.pdf" target="_blank">PDF version</a></p>
     $if(abstract)$
     <h3 class="text-center">Abstract</h3>
     <p class="text-justify">$abstract$</p>