cosas

nafems4.md

@@ -366,7 +366,7 @@ Three-dimensional unstructured tetrahedra-based grid for the system shown in\ [@
 :::::
 
 
-![Location of the six SCLs defined to analyse fatigue around the junction.](weldolet-scls.png){#fig:weldolet-scls}
+![Location of the six SCLs defined to analyse fatigue around the junction.](weldolet-scls.png){#fig:weldolet-scls width=75%}
 
 
 On the one hand, a reasonable number of nodes (remember it is the number of nodes that defines the problem size, not the number of elements) in order to get a decent grid is around 200k for each system. On the other hand, solving a couple of dozens of transient heat transfer problems (which we cannot avoid due to the large thermal inertia of the pipes) during a couple of thousands of seconds over a couple hundred of thousands of nodes might take more time and storage space to hold the results than we might expect.
@@ -382,13 +382,13 @@ dnl 33300 02-D-3-4
 
 
 ::::: {#fig:valve}
-![Full CAD model.](valve-cad1.png){#fig:valve-cad1}
+![Full CAD model.](valve-cad1.png){#fig:valve-cad1 width=80%}
 
-![Full mesh, approximately 220k nodes.](valve-mesh1.png){#fig:valve-mesh1}
+![Full mesh, approximately 220k nodes.](valve-mesh1.png){#fig:valve-mesh1 width=80%}
 
-![The SCLs are located at both sides of the material interface in the vertical plane both at the top and at the bottom of the pipe.](valve-scls1.png){#fig:valve-scls1}
+![The SCLs are located at both sides of the material interface in the vertical plane both at the top and at the bottom of the pipe.](valve-scls1.png){#fig:valve-scls1 width=75%}
 
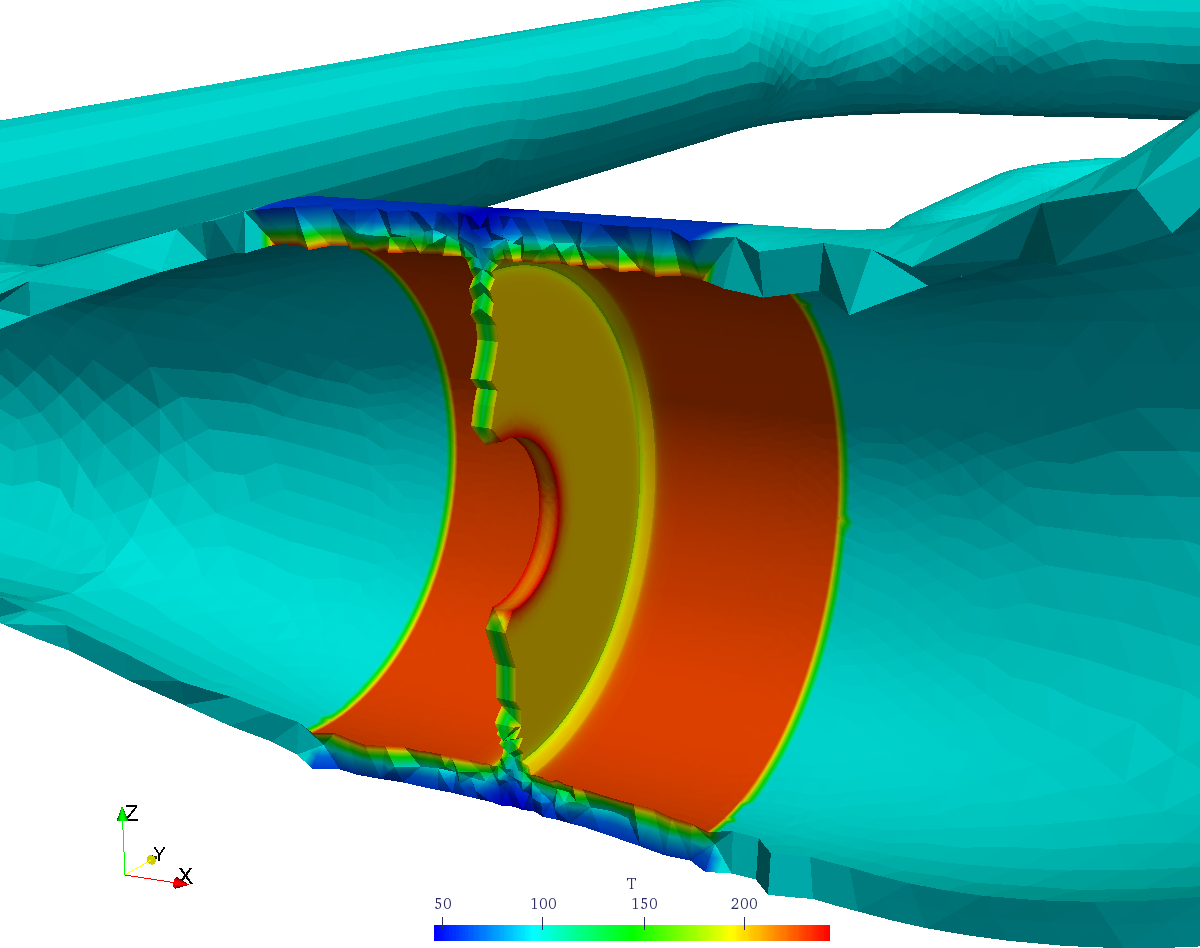
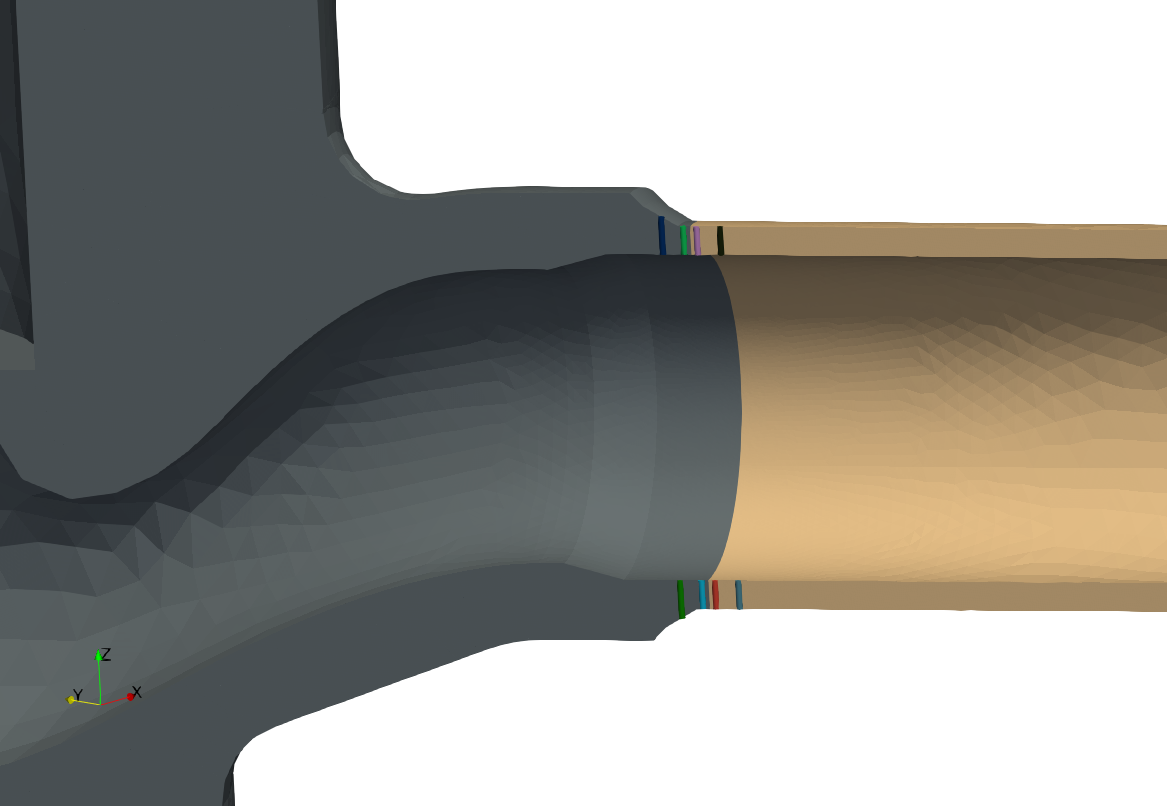
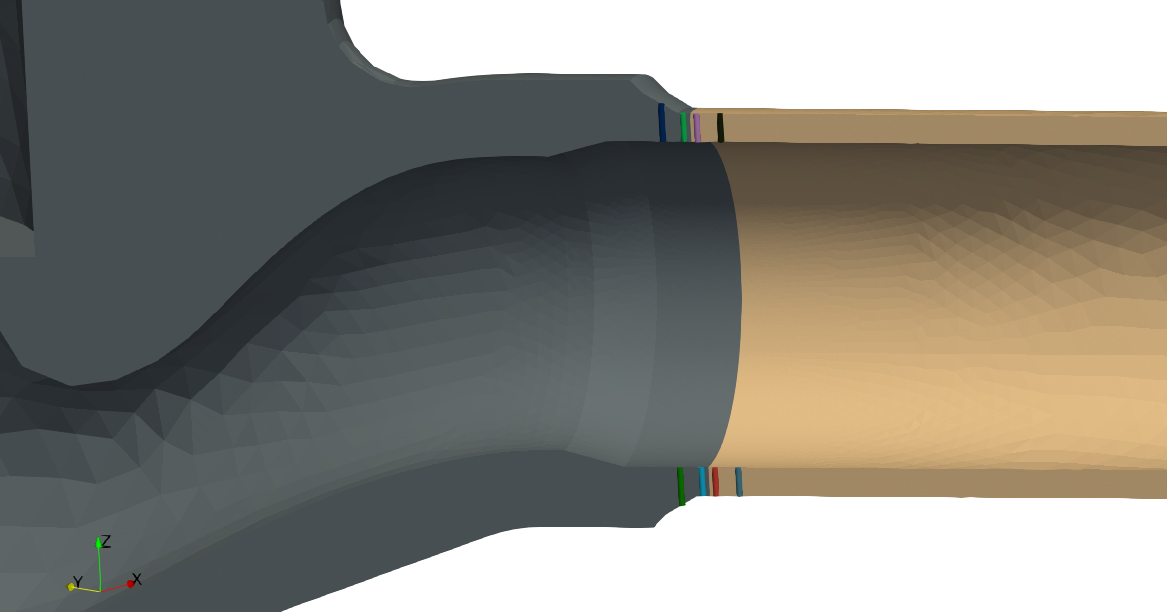
-An example case where the SCLs are located around the junction with the stainless-steel valves and the carbon steel pipe.
+An example case where the SCLs are located around the junction between stainless-steel valves and carbon steel pipes.
 :::::
 
 
@@ -396,7 +396,7 @@ An example case where the SCLs are located around the junction with the stainles
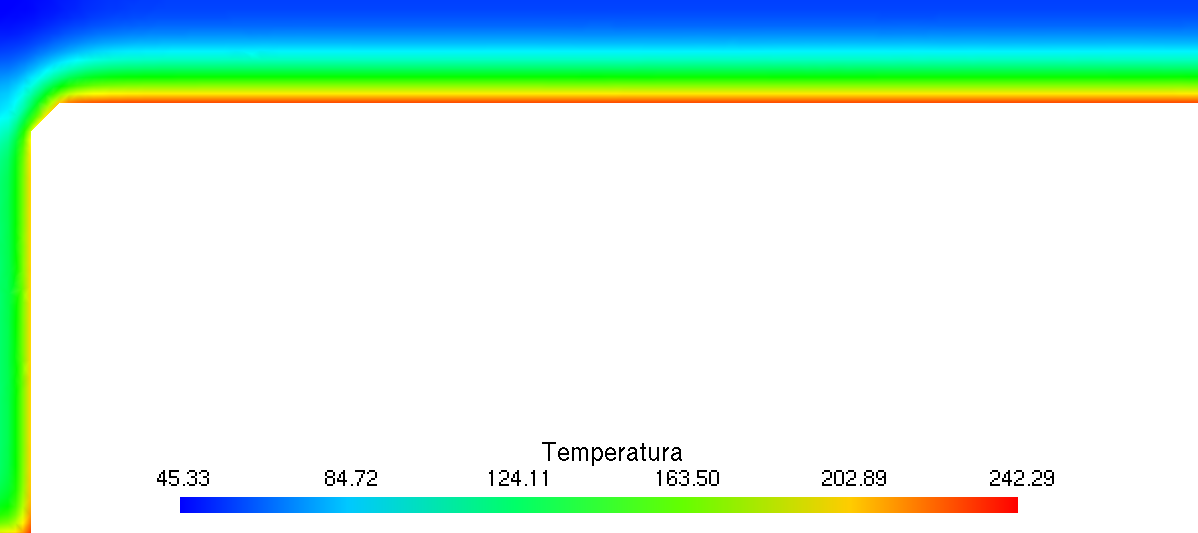
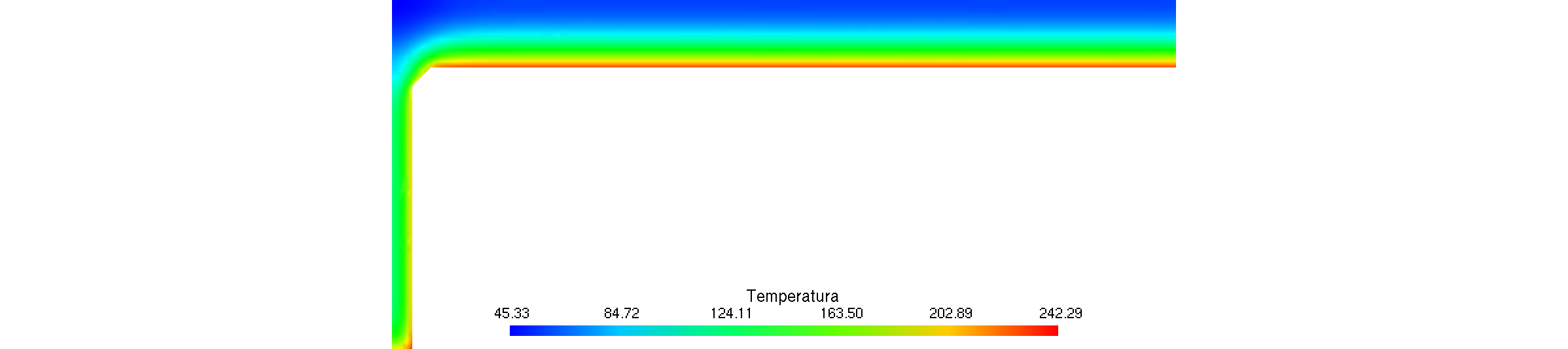
 As an example, let us consider the system depicted in\ [@fig:valve-cad1;fig:valve-scls1] where there is a stainless-carbon steel interface at the discharge of the valves. Instead of solving the transient heat-conduction problem with the internal temperature of the pipes equal to the temperature of the water in the reference transient condition of the power plant and an external condition of natural convection to the ambient temperature in the whole mesh of\ [@fig:valve-mesh1], a reduced model consisting of half of one of the two valves and a small length of the pipes at both the valve inlet and outlet is used. Once the temperature distribution\ $\hat{T}(\vec{x},t)$ for each time is obtained in the reduced mesh ([@fig:valve-temp], which has the origin at the center of the valve), the actual temperature distribution\ $T(\vec{x},t)$ is computed by an algebraic genearalisation of $\hat{T}(\vec{x},t)$ in the full coordinate system (where the origin is shown in\ [@fig:valve-cad1]). As stated above, those locations which are not covered by the reduced model are generalised with a time-dependent uniform temperature which is the average of the inner and outer temperatures at the inlet and outlet of the reduced mesh. The result is illustrated in figure\ [@fig:valve-gen].
 
 ::::: {#fig:valve-temp-gen}
-![Reduced mesh around the valve refined around the interface where the transient heat conduction problem is solved.](valve-temp.png){#fig:valve-temp}
+![Reduced mesh around the valve refined around the interface where the transient heat conduction problem is solved.](valve-temp.png){#fig:valve-temp width=80%}
 
 ![Generalization of the resulting temperature to the original mesh from figure [@fig:valve-mesh1]](valve-gen.png){#fig:valve-gen}
 
@@ -409,11 +409,11 @@ Please note that there is no need to have a one-to-one correspondence between th
 dnl 33410 10-12D-24
 
 ::::: {#fig:real}
-![Original full 3D mesh, carbon steel is magenta, stainless steel is green.](real-mesh2.png){#fig:real-mesh2}
+![Original full 3D mesh, carbon steel is magenta, stainless steel is green.](real-mesh2.png){#fig:real-mesh2 width=75%}
 
-![Temperature distribution for a certain time within the transient computed on a reduced two-dimensional axisymmetric mesh modeling half the orifice plate and a length of the carbon pipe.](real-temp.png){#fig:real-temp}
+![Temperature distribution for a certain time within the transient computed on a reduced two-dimensional axisymmetric mesh modeling half the orifice plate and a length of the carbon pipe.](real-temp.png){#fig:real-temp width=100%}
 
-![Generalization of the temperature obtained in the reduced mesh to the full three-dimensional grid.](real-gen.png){#fig:real-gen}
+![Generalization of the temperature from the reduced mesh to the full three-dimensional grid.](real-gen.png){#fig:real-gen width=80%}
 
 The material interface in the system from [@fig:real-life] is configured by an orifice plate made of stainless steel welded to a carbon-steel pipe.
 :::::
@@ -445,7 +445,7 @@ Practically, these problems are solved using the same mechanical finite-element
  1. The computation of the natural frequencies is “load free”, i.e. there can be no surface nor volumetric loads, and
  2. The displacement boundary conditions ought to be homogeneous, i.e. only displacements equal to zero can be given. One may fix only one of the three degrees of freedom in certain surfaces and leave the others free though, as long as all the rigid body motions are removed as usual.
 
-A real continuous solid has infinite modes of oscillation. A discretized one has three times the number of nodes modes of oscillation. In any case, one is usually interested only in a few of them, namely those with the lower frequencies because they take most of the energy with them. Each mode has two associated parameters called modal mass and excitation parameter that reflect how “important” the mode is regarding the absorption of energy from an external oscillatory source. Usually a couple of dozens of modes are enough to take up more than 90% of the earthquake energy. Figure\ [-@fig:modes] shows the first six natural modes of a sample piping section.
+A real continuous solid has infinite modes of oscillation. A discretized one (using the most common and efficient FEM formulation, the [displacement-based formulation](http://web.mit.edu/kjb/www/Books/FEP_2nd_Edition_4th_Printing.pdf)) has three times the number of nodes modes of oscillation. In any case, one is usually interested only in a few of them, namely those with the lower frequencies because they take most of the energy with them. Each mode has two associated parameters called modal mass and excitation parameter that reflect how “important” the mode is regarding the absorption of energy from an external oscillatory source. Usually a couple of dozens of modes are enough to take up more than 90% of the earthquake energy. Figure\ [-@fig:modes] shows the first six natural modes of a sample piping section.
 
 ::::: {#fig:modes}
 ![$i=1$](mode1.png){width=50%}
@@ -692,8 +692,8 @@ The first thing that has to be said is that, as with any interesting problem, th
  10. etc.
 
 ::::: {#fig:quarter}
-![Quarter-symmetry structured second-order incomplete hexahedra](quarter-struct.png){#fig:cube-struct width=48%}
-![Quarter-symmetry unstructured second-order tetrahedra](quarter-caeplex.png){#fig:quarter-caeplex width=48%}
+![Structured second-order incomplete hexahedra](quarter-struct.png){#fig:cube-struct width=48%}
+![Unstructured second-order tetrahedra](quarter-caeplex.png){#fig:quarter-caeplex width=48%}
 
 Two of the hundreds of different ways the infinite pressurized pipe can be solved using FEM
 :::::
@@ -725,7 +725,7 @@ Error in the computation of the linearised stresses vs. CPU time needed to solve
 
 ## Elements, nodes and CPU
 
-The last two bullets above lead to an issue that has come many times when discussing the issue of convergence with respect to the mesh size with other colleagues. There apparently exists a common misunderstanding that the number of elements is the main parameter that defines how complex a FEM model is. This is strange, because even in college we are taught that the most important parameter is the size of the stiffness matrix, which is three times (for 3D problems) the number of _nodes_.
+The last two bullets above lead to an issue that has come many times when discussing the issue of convergence with respect to the mesh size with other colleagues. There apparently exists a common misunderstanding that the number of elements is the main parameter that defines how complex a FEM model is. This is strange, because even in college we are taught that the most important parameter is the size of the stiffness matrix, which is three times (for 3D problems with the [displacement-based formulation](http://web.mit.edu/kjb/www/Books/FEP_2nd_Edition_4th_Printing.pdf) formulation) the number of _nodes_.
 
 Let us pretend we have to compare two different FEM programs so we solve the same problem in each and see what the results are. I have seen many times the following situation: the user loads the same geometry in both programs, meshes them so that the number of elements is more or less them same (because she wants to be “fair”) and solve the problem. Voilà! It turns out that the first program defaults to first-order elements and the second one to second-order elements. So if the first one takes one minute to obtain a solution, the second one should take nearly four minutes. How come that is a fair comparison? Or it might be the case that one program uses tetrahedra while the other one hexahedra. Or any other combination. In general, there is no single problem parameter that can be fixed to have a “fair” comparison, but if there were it would definetely be the number of nodes rather than the number of elements. Let us see why.
 
@@ -756,9 +756,7 @@ The linear FEM problem leads of course of a system of\ $NG$ linear equations, ca
 
 $$K \cdot \vec{u} = \vec{b}$$
 
-The objective of the solver is to find the vector\ $u$ of nodal displacements that satisfies the momentum equilibriums.
-
-Luckily (well, not purely by chance but by design) the stiffness matrix is almost empty. It is called a [sparse matrix](https://en.wikipedia.org/wiki/Sparse_matrix) because most of its elements are zero. If it was fully filled, then a problem with just 100k nodes would need more than 700\ Gb of RAM just to store the matrix elements, rendering FEM as practically impossible. And even though the stiffness matrix is sparse, its inverse is not so we cannot solve the elastic problem by “inverting” the matrix. Particular methods to represent and more importantly to solve linear systems involving these kind of matrices have been developed, which are the methods used by finite-element (and the other finite-cousins) programs. These methods are [iterative](https://en.wikipedia.org/wiki/Iterative_method) in nature, meaning that at each step of the iteration the numerical answer improves, i.e. $\left|K \cdot \vec{u} - \vec{b}\right| \rightarrow 0$. Even though in particular for [Krylov-subspace](https://en.wikipedia.org/wiki/Krylov_subspace) methods, $K \cdot \vec{u} - \vec{b} = \vec{0}$ after\ $NG$ steps, a few dozen of iterations are usually enough to assume that the problem is effectively solve (i.e. the residual is less than a certain threshold).
+The objective of the solver is to find the vector\ $u$ of nodal displacements that satisfies the momentum equilibriums. Luckily (well, not purely by chance but by design) the stiffness matrix is almost empty. It is called a [sparse matrix](https://en.wikipedia.org/wiki/Sparse_matrix) because most of its elements are zero. If it was fully filled, then a problem with just 100k nodes would need more than 700\ Gb of RAM just to store the matrix elements, rendering FEM as practically impossible. And even though the stiffness matrix is sparse, its inverse is not so we cannot solve the elastic problem by “inverting” the matrix. Particular methods to represent and more importantly to solve linear systems involving these kind of matrices have been developed, which are the methods used by finite-element (and the other finite-cousins) programs. These methods are [iterative](https://en.wikipedia.org/wiki/Iterative_method) in nature, meaning that at each step of the iteration the numerical answer improves, i.e. $\left|K \cdot \vec{u} - \vec{b}\right| \rightarrow 0$. Even though in particular for [Krylov-subspace](https://en.wikipedia.org/wiki/Krylov_subspace) methods, $K \cdot \vec{u} - \vec{b} = \vec{0}$ after\ $NG$ steps, a few dozen of iterations are usually enough to assume that the problem is effectively solve (i.e. the residual is less than a certain threshold).
 
 So the question is... how hard is to solve a sparse linear problem? Well, the number of iterations needed to attain convergence depends on the [spectral radius](https://en.wikipedia.org/wiki/Spectral_radius) of the stiffness matrix\ $K$, which in turns depend on the elements themselves, which depend mainly on the parameters of the elastic problem. But it also depends on how sparse\ $K$ is, which changes with the element topology and order. [@Fig:test] shows the structure of two stiffness matrices for the same linear elastic problem discretized using exactly the same number of nodes with first and second-order elements. The matrices have the same size (because the number of nodes is the same) but the former is more sparse than the latter. Hence, it would be harder (in computational terms of CPU and RAM) to solve the second-order case.
 
@@ -773,26 +771,85 @@ In a similar way, different types of elements will give rise to different sparsi
 
 ### Stress computation
 
-In the most common FEM formulation, the solver just “solves” for the displacements\ $\vec{u}(\vec{x})$ which are the principal unknowns. But from\ [@sec:tensor] we know that we actually “solve” the problem when we have the stress tensors at every location\ $\vec{x}$, which are the secondary unknowns. So the FEM program has to compute the stresses from the displacements using the materials’ constitutive equations which involve the Young Modulus\ $E$, the Poisson ratio\ $\nu$ and the spatial derivatives of the displacements\ $\vec{u}$. This sounds easy, as we (well, the solver) knows what the shape functions are for each element and then it is a matter of computing nine derivatives (that of the three displacements in each of the three directions) and multiplying by something involving\ $E$ and\ $\nu$. Yes, but there is a catch. As the displacements\ $u$ are computed at the nodes, we would like to also have the stresses at the nodes. But
+In the [displacement-based formulation](http://web.mit.edu/kjb/www/Books/FEP_2nd_Edition_4th_Printing.pdf), the solver just “solves” for the displacements\ $\vec{u}(\vec{x})$ which are the principal unknowns. But from\ [@sec:tensor] we know that we actually “solve” the problem when we have the stress tensors at every location\ $\vec{x}$, which are the secondary unknowns. So the FEM program has to compute the stresses from the displacements using the materials’ constitutive equations which involve the Young Modulus\ $E$, the Poisson ratio\ $\nu$ and the spatial derivatives of the displacements\ $\vec{u}$. This sounds easy, as we (well, the solver) knows what the shape functions are for each element and then it is a matter of computing nine derivatives (that of the three displacements in each of the three directions) and multiplying by something involving\ $E$ and\ $\nu$. Yes, but there is a catch. As the displacements\ $u$ are computed at the nodes, we would like to also have the stresses at the nodes. However,
 
  i. the displacements\ $\vec{u}(\vec{x})$ are not differentiable at the nodes, and
  ii. if the node belongs to a material interface, the\ $E$ and\ $\nu$ stuff is not defined.
 
-Let us focus on the first item and leave the second one for a separate discussion in\ [@sec:two-materials]. The finite-element method computes the principal unknowns at the nodes and then says “interpolate the nodal values inside each element using its shape functions.” It sounds (and it is) great, but a node belongs to more than one element. So the slope of the interpolation when we move from the node into one element might (and it never is) the same as when we move from the same node into another element. Neither in linear, nor quadratic nor higher-order elements. So what is the derivative of the displacement\ $v$ in the\ $y$ direction with respect to the $z$ coordinate? One answer would be the average of the derivatives computed in each of the elements that share a common node. But what if one of the elements is very small? Or it has a very bad quality (i.e. it is deformed in one direction) its derivatives cannot be trusted? Should the “average” be weighted? How?
+Let us focus on the first item and leave the second one for a separate discussion in\ [@sec:two-materials]. The finite-element method computes the principal unknowns at the nodes and then says “interpolate the nodal values inside each element using its shape functions.” It sounds (and it is) great, but a node belongs to more than one element (you can now imagine a 3D mesh composed of tetrahedra but you can also simplify your mind pictures by thinking in just one dimension: a node is shared by two segments). So the slope of the interpolation when we move from the node into one element might (and it never is) the same as when we move from the same node into another element. Neither in linear, nor quadratic nor higher-order elements. So what is the derivative of the displacement\ $v$ in the\ $y$ direction with respect to the $z$ coordinate? One answer would be the average of the derivatives computed in each of the elements that share a common node. But what if one of the elements is very small? Or it has a very bad quality (i.e. it is deformed in one direction) its derivatives cannot be trusted? Should the “average” be weighted? How?
 
 **FIGURA 1D**
 
-inside elements at gauss points
+Math shows that the location where the derivatives of the interpolated displacements are closer to the real (i.e. the analytical in problem that have it) solution are the elements’ [Gauss points](https://en.wikipedia.org/wiki/Gaussian_quadrature). Even better, the material properties at these points are continuous (they are usually uniform but they can depend on temperature for example) because, unless we are using weird elements, there are no material interfaces inside elements. But how to manage a set of stresses given at the Gauss points instead of at the nodes? Should we use one mesh for the input and another one for the output? What happens when we need to know the stresses on a surface and not just in the bulk of the solid? There are still no one-size-fits-all answers.
 
+In any case, this step takes a non-negligible amount of time. The most-common approach, i.e. the node-averaging method is driven mainly by the number of nodes of course. So all-in-all, these are the reasons to use the number of nodes instead of the numbers of elements as a basic parameter to measure the complexity of a FEM problem.
 
 
 ## Two (or more) materials {#sec:two-materials}
 
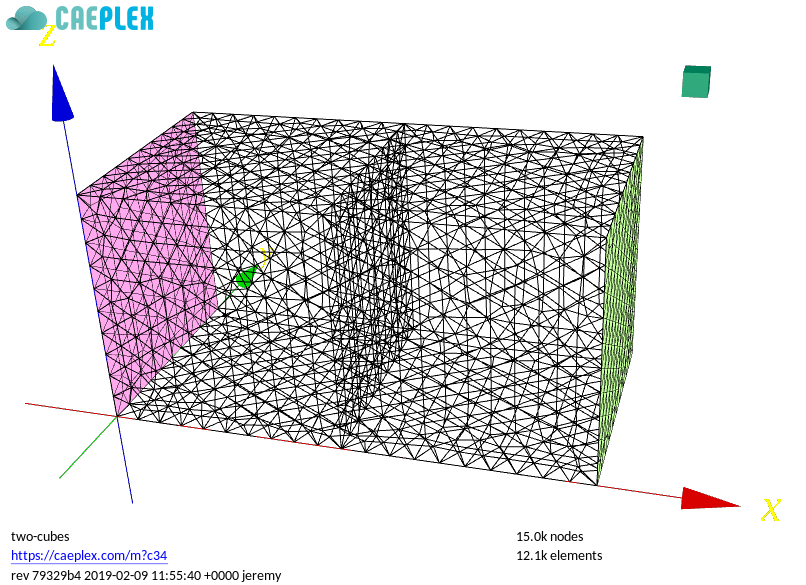
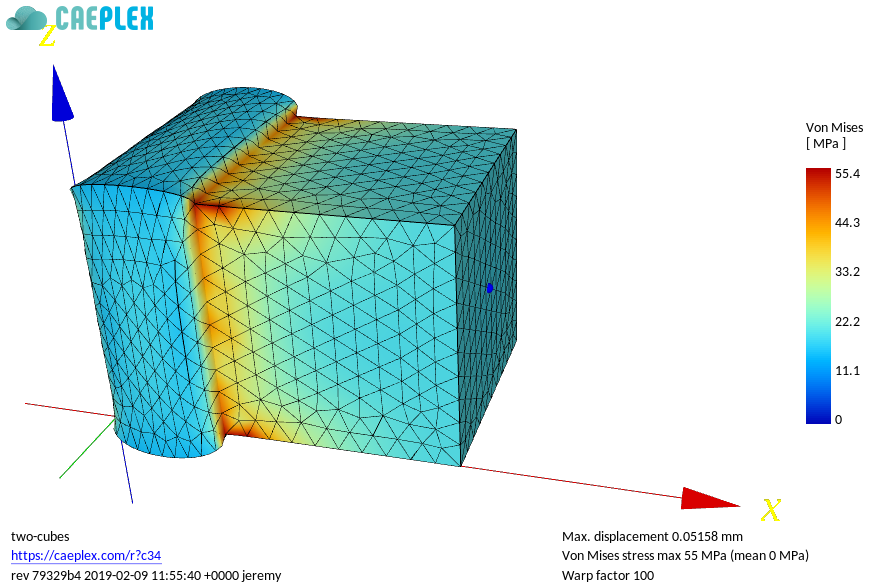
+The main issue with fatigue in nuclear piping during operational transients is that at the welds between two materials with different thermal expansion coefficients there can appear potentially-high stresses during temperature changes. If these transients are repeated cyclically, fatigue may occur. We already have risen a warning flag about stresses at material interfaces. Besides all the open questions about computing stresses at nodes, this case also adds the fact that the material properties (say the Young Modulus\ $E$) is different in the elements that are at each side of the interface.
+
+::::: {#fig:test}
+![Surface grid showing the fixed face (magenta), the load face (green) and the shared face in the middle.](two-cubes2.png){#fig:two-cubes2 width=48%}
+![Warped displacements and Von Mises stresses.](two-cubes4.png){#fig:two-cubes2 width=48%}
+
+Two cubes of different materials (the one in the left soft, the one in the right hard) share a face and a pressure is applied at the right-most face.
+:::::
+
+
+To simplify the discussion that follows, let us replace for one moment all the full $3 \times 3$ tensor and the nine partial derivatives of the displacement by just one strain\ $\epsilon$ and let the strain-stress relationship to be the scalar expression
+
+$$
+\sigma = E \cdot \epsilon
+$$
+
+Faced with the problem of computing the stress\ $\sigma$ at one node shared by many elements, we might:
+
+ 1. compute the (weighted?) averages\ $\langle E \rangle$ and $\langle \epsilon \rangle$ and then compute the stress as
+
+    $$ \langle \sigma \rangle = \langle E \rangle \cdot \langle \epsilon \rangle$$
+
+ This would be like having a meta-material at the interface with average properties, or
+
+ 2. compute the stress as the (weighted?) average of the product $E \cdot \epsilon$ in each node
+
+    $$ \langle \sigma \rangle = \langle E \cdot \epsilon \rangle$$
+
+ This would be like forcing a non-differentiable function to behave smoothly, or
+
+ 3. internally duplicate the nodes at the interface and compute one stress for each material. This would result in a stress distribution which is not a real function because the same location\ $\vec{x}$ will be associated to more than one stress value, or
+
+ 4. duplicate the surface elements at the interfaces and solve the problem using a contact formulation. This would render the problem non-linear add the complexity of having to find appropriate penalty coefficients.
+
+There might be other choices as well. Do you know what your favourite FEM program does? Now follow up with these questions:
+
+ a. Does the manual say?
+ b. Does it tell you the details like how it weights the averages?
+ c. Does it throw away values that are beyond a number of standard deviations away?
+ d. How many standard deviations?
+ e. ...
+
+
+You can still add a lot of questions that you should be having right now. After you do, add another one:
+
+ * Do you believe the manual?
+
+If you cannot get a clear answer for at least one of them, then start to be worried. Maybe it is time to change your favourite FEM program?
+
+What we as fully cognizant engineers that have to sign a report stating that a nuclear power plant will not collapse due to fatigue in its pipes is to fully understand what is going on with our stresses. [Richard Stallman](https://en.wikipedia.org/wiki/Richard_Stallman) says that the best way to solve a problem is to avoid it in the first place. In this case, we should avoid having to trust to a written manual and rely on software whose [source code](https://en.wikipedia.org/wiki/Source_code) is available. What we need is the capacity (RMS calls it _freedom_) to be able to see the detailed steps performed by the program so we can answer any question we (or other people) might have.
+
+Without resorting into philosophical digressions about the difference between [free and open-source software](https://en.wikipedia.org/wiki/Free_and_open-source_software) (not because it is not worth it but because it would take a whole book), the programs that make their source code available for their users are called [open-source software](https://en.wikipedia.org/wiki/Open-source_software). If the users can also modify and re-distribute the modified versions are called 
+
+So you do not how to program and th
+
 open source!
 que hacen los programas? NADIE SABE
 
 two cubes
 
+todo esto es para una interfaz abrupta, en realidad hay HAZ, cambio de estructura, etc
+SCLs a una distancia (engineering)
+
 ## A parametric tee
 
 ## Bake, shake and break {#sec:break}
@@ -819,8 +876,9 @@ Back in College, we all learned how to solve engineering problems. But there is
  * grab any stress distribution from any of your FEM projects, compute the iso-stress curves and the draw normal lines to them to get acquainted with SCLs
  * first search online for “stress linearisation” (or “linearization” if you want) and then get a copy of ASME\ VIII Div\ 2 Annex 5-A
  * try to show that even though the principal stresses are not linear with respect to summation, they are linear with respect to multiplication (with pencil and paper)
- * learn by heart: the complexity of a FEM problem is given mainly but the number of nodes, not by the number of elements
  * measure the time needed to generate grids of different sizes and kinds with your favourite mesher
+ * learn this by heart: the complexity of a FEM problem is given mainly but the number of nodes, not by the number of elements
+ * welded materials with different thermal expansion coefficients may lead to fatigue under cyclic temperature changes