+ 24
- 5
nafems4.md
查看文件
| @@ -32,7 +32,7 @@ In the years following Enrico Fermi’s demonstration that a self-sustainable fi | |||
| After further years passed by, engineers (probably the same people that forked section\ III) noticed that fatigue in nuclear power plants was not exactly the same as in other piping systems. There were some environmental factors directly associated to the power plant that was not taken into account by the regular ASME code. Again, instead of writing a new code from scratch, people decided to add correction factors to the previously amended body of knowledge. This is how knowledge evolves, and it is this kind of complexities that engineers are faced with during their professional lives. We have to face it, it would be a very hard work to re-write everything from scratch every time something changes. | |||
|  | |||
|  | |||
| Actually, this article does not focus on a single case study but on some general ideas regarding analysis of fatigue in piping systems in nuclear power plants. There is no single case study but a compendium of ideas obtained by studying many different systems which are directly related to the safety of a real nuclear reactor. | |||
| @@ -237,7 +237,7 @@ This kind of computation is usually required by the nuclear regulatory authoriti | |||
| **------** | |||
| ## Five whys do you want to do FEA? | |||
| ## Five whys {#sec:five} | |||
| So we know we need a numerical scheme to solve our mechanical problem because anything slightly more complex than an infinite pipe does not have analytical solution. We need an unstructured grid because we would not use Legos to discretise pipes. We selected the finite elements method over the finite volumes method, because FEM is the king. Can we pause again and ask ourselves why is it that we want to do finite-element analysis? | |||
| @@ -321,10 +321,29 @@ So we need to address the issue of fatigue in nuclear reactor pipes that | |||
| b. heat transients, and | |||
| c. seismic loads. | |||
| Due to 1--3, it is clear we need to use finite elements to solve the elastic problem to obtain the stress tensor which would go into the fatigue curves. Now, even though the nature of the load is time-dependent, the time scale of the phenomena is rather different and should be separately analyzed. | |||
| As I wanted to illustrate in [@sec:five], it is very important to decide what kind of problem (actually problems) we should be dealing with. As a nuclear engineer, I learned (after college) that there are some models that let you see some effects and some that let you see other effects.^[Please [say “modeling” not “simulation.”](https://www.seamplex.com/blog/say-modeling-not-simulation.html)] And even if it is in principle true that more complex models should let you see more stuff, they practically might show you nothing at all if the model is so big and complex that cannot fit into a computer (say because it needs hundreds of gigabytes of RAM to run) or because it takes more time to compute than you may have to deliver a report. | |||
| First, the pressure transient | |||
| First of all, we should note that we need to solve | |||
| i. the heat transfer equation to get the temperature distribution within the pipes, | |||
| ii. a frequency analysis of the piping system to get the natural oscillation modes and use them to obtain the pseudo-accelerations created by the design earthquake, and finally | |||
| iii. the elastic problem to obtain the stress tensor needed to compute the alternating stress to enter into the fatigue curve. | |||
| So for each time of the transient, the pipes are subject to | |||
| a. an uniform internal pressure\ $p_i(t)$ that depends on time, | |||
| b. a uniform internal temperature $T_i(t)$ that gives rise to a non-trivial time-dependent temperature distribution\ $T(\vec{x},t)$ in the bulk of the pipes, and | |||
| c. internal distributed forces\ $\vec{f}=\rho \cdot \vec{a}$ at those times where the design earthquake is assumed to act. | |||
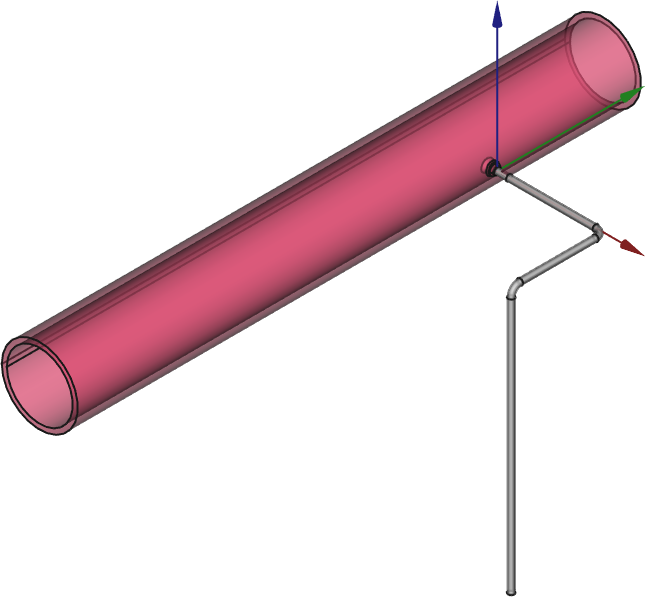
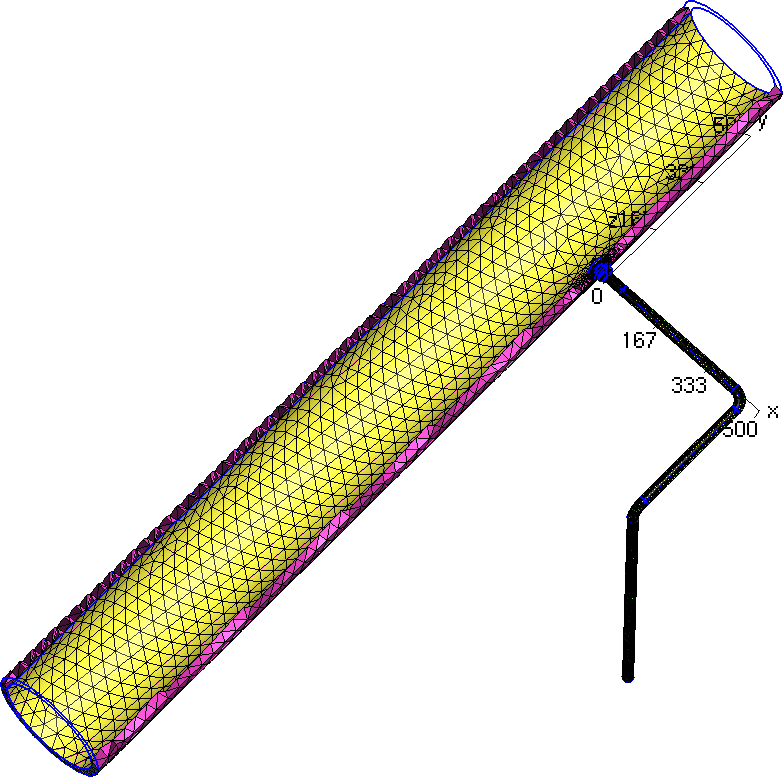
| Remember the main issue of the fatigue analysis in these systems is to analyse what happens around change of piping classes where different materials (i.e. different expansion coefficients) are present, potentially causing high stresses due to differential thermal expansion (or contraction) in transient conditions. Therefore, even though we are dealing with pipes we cannot use beam or circular shell elements, because we need to take into account the three-dimensional effects of the temperature distribution along the pipe thickness. And even if it we could, there are some tees that connect pipes with different nominal diameters that have a non-trivial geometry, such as the weldolet-type junction shown in\ [@fig:weldolet-cad1;@fig:weldolet-mesh2]. | |||
| {#fig:weldolet-cad1} | |||
| {#fig:weldolet-cad2} | |||
| {#fig:weldolet-mesh1} | |||
| {#fig:weldolet-mesh2} | |||
| ## The infinite pipe revisited after college | |||
| @@ -365,7 +384,7 @@ cantilever beam, principal stresses, linearity of von mises | |||
| ## Two (or more) materials | |||
| ### Young and Poisson | |||
| / | |||
| two cubes | |||
| ## A parametric tee | |||
cad1.png → real-piping.png
查看文件
二進制
weldolet-cad1.png
查看文件
二進制
weldolet-cad2.png
查看文件
二進制
weldolet-mesh1.png
查看文件
二進制
weldolet-mesh2.png
查看文件
Loading…