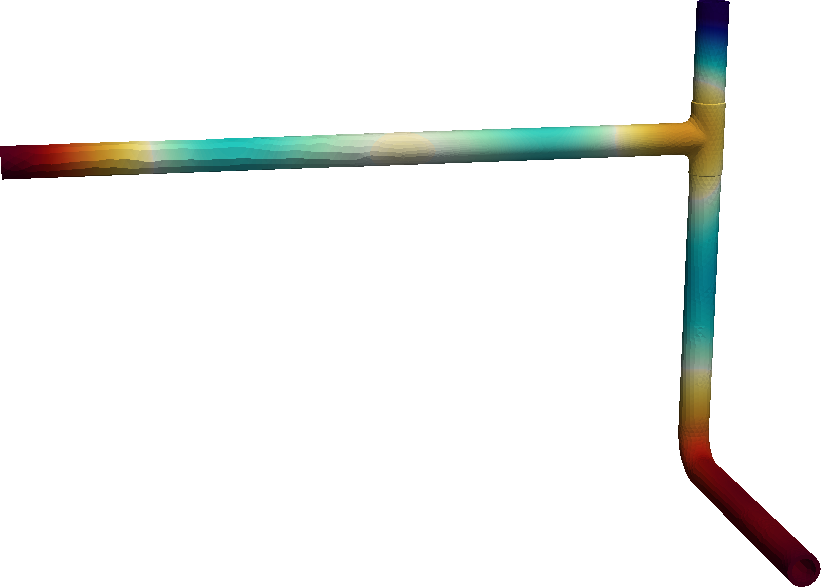espectro

nafems4.md

@@ -457,7 +457,7 @@ In case you are wondering, the answer is yes: all nuclear power plants are desig
 
 Back to our case study, the point is that each site where nuclear power plants are built must have a geological study where a postulated design-basis earthquake is to be defined. In other words, a theoretical earthquake which the plant ought to withstand needs to be specified. How? By giving a set of three spectra (one for each coordinate direction) giving acceleration as a function of the frequency for each level of the building. That is to say, once the earthquake hits the power plant, depending on soil-structure interactions the energy will shake the building foundations in a way that depends on the characteristics of the earthquake, the soil and the concrete structure. Afterwards, they way the oscillations travel upward and shake each of the mechanical components erected in each floor level depends on the design of the civil structure in a way which is fully determined by the floor response spectra like the ones depicted in\ [@fig:spectrum].
 
-![A sample spectrum for a certain floor level of a certain nuclear power plant.](spectrum.vector_format){#fig:spectrum}
+![A sample spectrum for a certain floor level of a certain nuclear power plant.](spectrum.svg){#fig:spectrum}
 
 ### Natural frequencies
 
@@ -675,6 +675,10 @@ A \cdot B = B \cdot A
 $$
 then the sums of their eigenvalues are equal to the eigenvalues of the sums. In order for this to happen, both\ $A$ and\ $B$ need to be diagonalisable using the same basis. That is to say, the diagonalising matrix\ $P$ such that $P^{-1} A P$ is diagonal is the same that renders\ $P^{-1} B P$ also diagonal. What does this mechanically mean? Well, if case\ A has loads that are somehow “independent” from the ones in case\ B, then the principal stresses of the combination might be equal to the sum of the individual principal stresses. A notable case is for example a beam that is loaded vertically in case\ A and horizontally in case\ B. I dare you to grab your FEM program one more time, run a test and picture the eigenvalues and eigenvectors of the three cases in your head.
 
+\medskip
+
+The moral of this fable is that if we have a case that is the combination of two other simpler cases (say one with only surface loads and one with only volumetric loads), in general we cannot just add the stresses and expect to obtain the correct principal stresses. We have to solve the full case again (both the surface and the volumetric loads at the same time). In case we are stubborn enough and still want to stick to solving the cases separately, there is a trick we can resort to. Instead of summing stresses, what we can do is to sum displacements which are fully linear. So we might pre-deform case B with the results from case A and then expect to obtain the correct stresses for the combined case. However, this scheme is actually far more complex than just solving the combined case in a single run and it also needs an educated guess and/or trial and error to know at what time the pre-deformation should be applied to take into account the seismic load.
+
 
 ## ASME stress linearisation (not linearity!)
 
@@ -1022,32 +1026,45 @@ Temperature distribution for a certain instant of the transient, computed in the
 :::::
 
 ::::: {#fig:case-mode}
-![$i=1$](case-mode1.png){#fig:case-mode-1 width=30%}\ 
-![$i=2$](case-mode2.png){#fig:case-mode-2 width=30%}\ 
-![$i=3$](case-mode3.png){#fig:case-mode-3 width=30%} 
+![$i=1$](case-mode1.png){#fig:case-mode-1 width=30%}\  
+![$i=2$](case-mode2.png){#fig:case-mode-2 width=30%}\  
+![$i=3$](case-mode3.png){#fig:case-mode-3 width=30%}  
 
-![$i=4$](case-mode4.png){#fig:case-mode-4 width=30%}\ 
-![$i=5$](case-mode5.png){#fig:case-mode-5 width=30%}\ 
-![$i=6$](case-mode6.png){#fig:case-mode-6 width=30%} 
+![$i=4$](case-mode4.png){#fig:case-mode-4 width=30%}\  
+![$i=5$](case-mode5.png){#fig:case-mode-5 width=30%}\  
+![$i=6$](case-mode6.png){#fig:case-mode-6 width=30%}
 
-![$i=7$](case-mode7.png){#fig:case-mode-7 width=30%}\ 
-![$i=8$](case-mode8.png){#fig:case-mode-8 width=30%}\ 
+![$i=7$](case-mode7.png){#fig:case-mode-7 width=30%}\  
+![$i=8$](case-mode8.png){#fig:case-mode-8 width=30%}\  
 ![$i=9$](case-mode9.png){#fig:case-mode-9 width=30%}
 
-First nine natural modes of oscillation of the piping system subject to the boundary conditions the supports provide. 
+First nine natural modes of oscillation of the piping system subject to the boundary conditions the supports provide.
+:::::
+
+![Floor response spectrum.](case-spectrum.svg){#fig:case-spectrum width=80%}
+
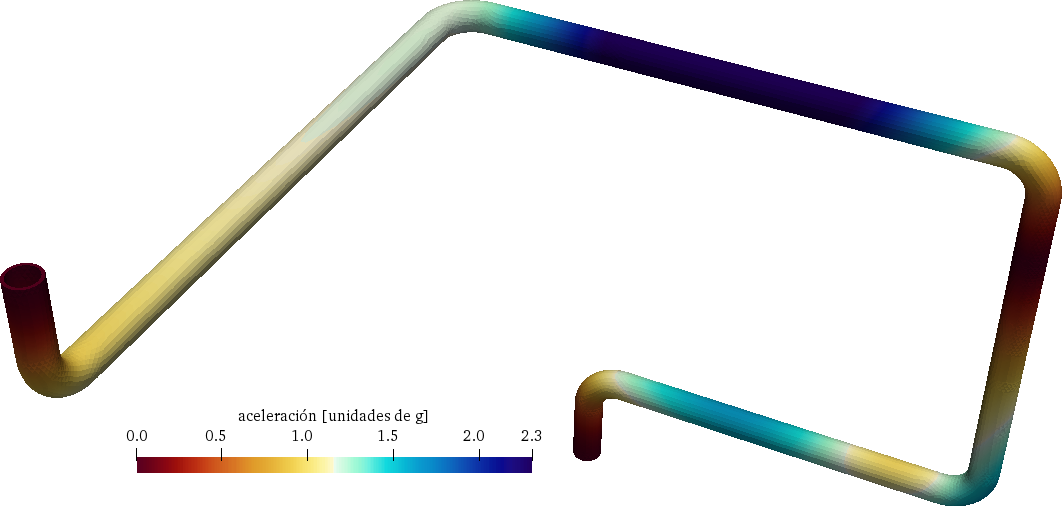
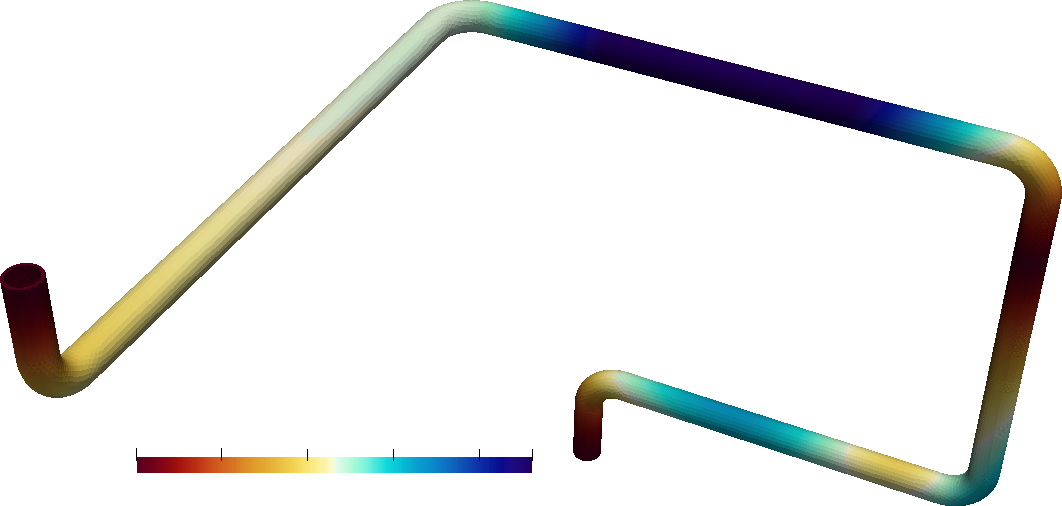
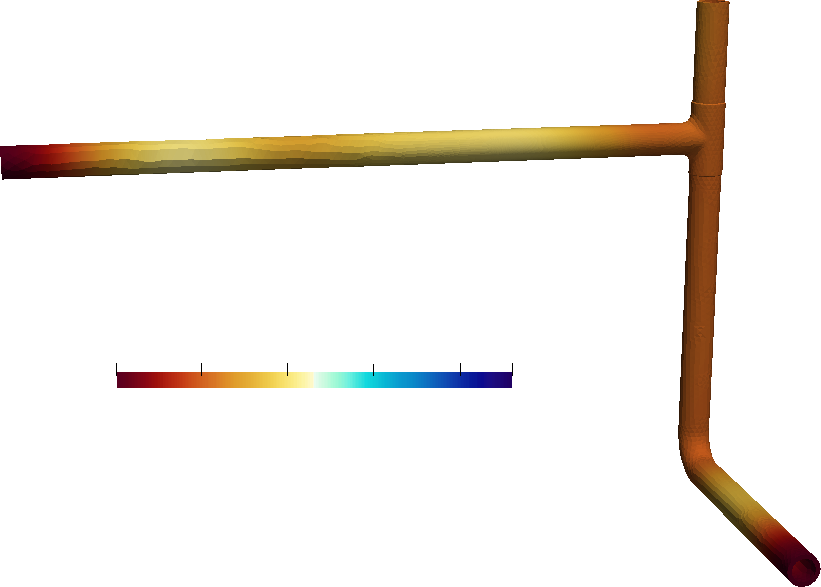
+::::: {#fig:case-acceleration}
+![$a_x$](case-ax.png){width=50%}
+
+![$a_y$](case-ay.png){width=50%}
+
+![$a_z$](case-az.png){width=50%}
+
+The static equivalent accelerations for the spectra of\ [@fig:case-spectrum] computed using the SRSS method.
 :::::
 
+
 \medskip
 
-To recapitulate, here are some partial non-dimensional results of an actual system of a certain nuclear power plant. The main issues to study were the interfaces between a carbon-steel pipe and a stainless-steel orifice plate used to measure the (heavy) water flow through the line. The steps discussed so far include 
+To recapitulate, here are some partial non-dimensional results of an actual system of a certain nuclear power plant. The main issues to study were the interfaces between a carbon-steel pipe and a stainless-steel orifice plate used to measure the (heavy) water flow through the line. The steps discussed so far include
 
- 1. building a CAD model of the piping section under study (main domain)
- 2. creating a mesh for the main domain refining locally around the material interfaces
- 3. defining the number and locations of the SCLs
- 4. computing a heat conduction transient problem with temperatures as a function of time from the operational transient in a simple domain using temperature-dependent thermal conduction coefficients from ASME\ II (bake)
- 5. generalising the temperature distribution as a function of time to the general domain
- 6. performing a modal analysis on the main domain to obtain the main oscillation frequencies and modes (shake)
- 7. using the floor response spectra and the SRSS method to obtain a distributed force statically-equivalent to the earthquake load (not shown)
+ 1. building a CAD model of the piping section under study, which will be the main domain ([@fig:case-cad] or [@fig:real-life;@fig:weldolet-cad;@fig:valve-cad1])
+ 2. creating a mesh for the main domain refining locally around the material interfaces ([@fig:case-mesh] or [@fig:weldolet-mesh;@fig:valve-mesh1;@fig:real-mesh2])
+ 3. defining the number and locations of the SCLs ([@fig:case-scls] or [@fig:weldolet-scls;@fig:valve-scls1;@fig:tee-scls])
+ 4. computing a heat conduction (bake) transient problem with temperatures as a function of time from the operational transient in a simple domain using temperature-dependent thermal conduction coefficients from ASME\ II\ part D ([@fig:case-temp] or [@fig:valve-temp;@fig:real-mesh2])
+ 5. generalising the temperature distribution as a function of time to the general domain ([@fig:case-temp2] or [@fig:valve-gen;@fig:real-gen])
+ 6. performing a modal analysis (shake) on the main domain to obtain the main oscillation frequencies and modes ([@fig:case-mode] or [@fig:modes])
+ 7. using the floor response spectra ([@fig:case-spectrum] or [@fig:spectrum]) and the SRSS method to obtain a distributed force statically-equivalent to the earthquake load ([@fig:case-acceleration] or [@fig:acceleration])
  8. successively solving the linear elastic problem for different times using the generalised temperature distribution taking into account
      a. the dependence of the Young Modulus\ $E$ and the thermal expansion coefficient\ $\alpha$ with temperature,
      b. the thermal expansion effect itself
@@ -1059,9 +1076,9 @@ To recapitulate, here are some partial non-dimensional results of an actual syst
      b. Principal 2
      c. Principal 3
      d. Tresca
- 10. juxtaposing these linearised stresses for each time of the transient and for each transient so as to obtain a single time-history of stresses including all the operational and/or incidental transients under study, which is what fatigue analysis need (recall\ [@sec:fatigue]). 
+ 10. juxtaposing these linearised stresses for each time of the transient and for each transient so as to obtain a single time-history of stresses including all the operational and/or incidental transients under study, which is what fatigue analysis need (recall\ [@sec:fatigue]).
 
-A pretty nice list of steps, which definitely I would not have been able to tackle when I was in college. 
+A pretty nice list of steps, which definitely I would not have been able to tackle when I was in college. Would you?
 
 
 # Usage factors {#sec:usage}
@@ -1097,6 +1114,6 @@ Back in college, we all learned how to solve engineering problems. And once we g
  * learn this by heart: the complexity of a FEM problem is given mainly by the number of _nodes_, not by the number of elements
  * remember that welded materials with different thermal expansion coefficients may lead to fatigue under cyclic temperature changes
  * if you have time, try to get out of your comfort zone and do more than what other expect from you (like parametric computations)
- * clone the [parametric tee repository](https://bitbucket.org/seamplex/tee), understand how the figures from\ [@sec:parametric] where built and expand them to cover “we might go on...” bullets
- * think thermal-mechanical plus eartquakes as “bake, break and shake” problems
- * the elastic problem is still linear
+ * clone the [parametric tee repository](https://bitbucket.org/seamplex/tee), understand how the figures from\ [@sec:parametric] were built and expand them to cover “we might go on...” bullets
+ * think thermal-mechanical plus earthquakes as “bake, break and shake” problems
+ * the elastic problem is still linear after all