|
|
|
@@ -9,13 +9,18 @@ |
|
|
|
|
|
|
|
# CS4: Fatigue Assessment in Nuclear Piping |
|
|
|
|
|
|
|
## From college theory to an actual engineering problem |
|
|
|
## From college theory to an actual engineering problem {#sec:intro} |
|
|
|
|
|
|
|
First of all, please take this text as a written chat between you an me, i.e. an average engineer that has already taken the journey from college to performing actual engineering works using finite element analysis and has something to say about it. Picture yourself in a coffee bar, talking and discussing concepts and ideas with me. Maybe needing to go to a blackboard (or notepad?). Even using a tablet to illustrate some three-dimensional results. But always as a chat between colleagues. |
|
|
|
|
|
|
|
Please also note that I am not a mechanical engineer, although I shared many undergraduate courses with some of them. I am a nuclear engineer with a strong background in mathematics and computer programming. I went to college between 2002 and 2008. Probably a lot of things have changed since then---at least that is what these “millennial” guys and girls seem to be boasting about---but chances are we all studied solid mechanics and heat transfer with a teacher using a piece of chalk on a blackboard while we as students wrote down notes with pencils on paper sheets. And there is really not much that one can do with pencil and paper regarding mechanical analysis. Any actual case worth the time of an engineer needs to be more complex than an ideal canonical case with analytical solution. |
|
|
|
|
|
|
|
Whether you are a student or a seasoned engineer with many years of experience, you might recall from first year physics courses the introduction of the [simple pendulum](https://en.wikipedia.org/wiki/Pendulum) as a case study\ ([@fig:simple]). You learned that the period does not depend on the hanging mass because the weight and the inertia exactly cancelled each other. Also, that [Galileo](https://en.wikipedia.org/wiki/Galileo_Galilei) said (and [Newton proved](https://www.seamplex.com/wasora/realbook/real-012-mechanics.html)) that for small oscillations the period does not even depend on the amplitude. Someone showed you why it worked this way: because if\ $\sin \theta \approx \theta$ then the motion equations converge to an [harmonic oscillator](https://en.wikipedia.org/wiki/Harmonic_oscillator). It might have been a difficult subject for you back in those days when you were learning physics and calculus at the same time. You might have later studied the [Lagrangian](https://en.wikipedia.org/wiki/Lagrangian_mechanics) and even the [Hamiltonian](https://en.wikipedia.org/wiki/Hamiltonian_mechanics) formulations, added a [parametric excitation](https://en.wikipedia.org/wiki/Parametric_oscillator) and analysed the [chaotic double pendulum](https://www.seamplex.com/wasora/realbook/real-017-double-pendulum.html). But it was probably after college, say when you took your first son to a swing on a windy day ([@fig:hamaca]), that you were faced with a real pendulum worth your full attention. Yes, this is my personal story but it could have easily been yours as well. My point is that the very same distance between what I imagined studying a pendulum was and what I saw that day at the swing (namely that the period _does_ depend on the hanging mass) is the same distance between the mechanical problems studied in college and the actual cases encountered during a professional engineer’s lifetime ([@fig:pipes]). In this regard, I am referring only to technical issues. The part of dealing with clients, colleagues, bosses, etc. which is definitely not taught in engineering schools (you can get a heads up in business schools, but again it would be a theoretical pendulum) is way beyond the scope of both this article and my own capacities. |
|
|
|
Whether you are a student or a seasoned engineer with many years of experience, you might recall from first year physics courses the introduction of the [simple pendulum](https://en.wikipedia.org/wiki/Pendulum) as a case study\ ([@fig:simple]). You learned that the period does not depend on the hanging mass because the weight and the inertia exactly cancelled each other. Also, that [Galileo](https://en.wikipedia.org/wiki/Galileo_Galilei) said (and [Newton proved](https://seamplex.com/wasora/doc/realbook/012-mechanics/)) that for small oscillations the period does not even depend on the amplitude. Someone showed you why it worked this way: because if\ $\sin \theta \approx \theta$ then the motion equations converge to an [harmonic oscillator](https://en.wikipedia.org/wiki/Harmonic_oscillator). It might have been a difficult subject for you back in those days when you were learning physics and calculus at the same time. |
|
|
|
divert(-1) |
|
|
|
You might have later studied the [Lagrangian](https://en.wikipedia.org/wiki/Lagrangian_mechanics) and even the [Hamiltonian](https://en.wikipedia.org/wiki/Hamiltonian_mechanics) formulations, added a [parametric excitation](https://en.wikipedia.org/wiki/Parametric_oscillator) and analysed the [chaotic double pendulum](https://seamplex.com/wasora/doc/realbook/017-double-pendulum). divert(0) |
|
|
|
But it was probably after college, say when you took your first son to a swing on a windy day ([@fig:hamaca]), that you were faced with a real pendulum worth your full attention. |
|
|
|
dnl Yes, this is my personal story but it could have easily been yours as well. |
|
|
|
The very same distance between what I imagined studying a pendulum was and what I saw that day at the swing (namely that the period _does_ depend on the hanging mass) is the same distance between the mechanical problems studied in college and the actual cases encountered during a professional engineer’s lifetime ([@fig:pipes]). In this regard, I am referring only to technical issues. The part of dealing with clients, colleagues, bosses, etc. which is definitely not taught in engineering schools (you can get a heads up in business schools, but again it would be a theoretical pendulum) is way beyond the scope of both this article and my own capacities. |
|
|
|
|
|
|
|
::::: {#fig:pendulum} |
|
|
|
{#fig:simple width=35%}\ |
|
|
|
@@ -28,17 +33,18 @@ A [simple pendulum from college physics courses](https://www.seamplex.com/wasora |
|
|
|
{#fig:infinite-pipe width=40%} |
|
|
|
{#fig:isometric width=58%} |
|
|
|
|
|
|
|
An infinitely-long pressurised thick pipe as taught in college and an isometric drawing of a section of a real-life piping system |
|
|
|
An infinitely-long pressurised thick pipe as taught in college and an isometric drawing of a section of a real-life piping system. The details of the isometric are not important individually but they are included to emphasize the fact that a real engineering drawing is far more complex and has far more information than what a professor can draw in a class blackboard. |
|
|
|
::::: |
|
|
|
|
|
|
|
divert(-1) |
|
|
|
Like the pendulums above, we will be swinging back and forth between a case study about fatigue assessment of piping systems in a nuclear power plant and more generic topics related to finite elements and computational mechanics. These latter regressions will not remain just as abstract theoretical ideas. Not only will they be directly applicable to the development of the main case, but they will also apply to a great deal of other engineering problems tackled with the finite element method (and its cousins, [@sec:formulations]). |
|
|
|
|
|
|
|
\medskip |
|
|
|
|
|
|
|
Finite elements are like magic to me. I mean, I can follow the whole derivation of the equations, from the strong, weak and variational formulations of the equilibrium equations for the mechanical problem (or the energy conservation for heat transfer) down to the [algebraic multigrid](https://en.wikipedia.org/wiki/Multigrid_method) [preconditioner](https://en.wikipedia.org/wiki/Preconditioner) for the inversion of the [stiffness matrix](https://en.wikipedia.org/wiki/Stiffness_matrix) passing through [Sobolev spaces](https://en.wikipedia.org/wiki/Sobolev_space) and the [grid generation](https://en.wikipedia.org/wiki/Mesh_generation). Then I can sit down and program all these steps into a computer, including the [shape functions](https://en.wikipedia.org/wiki/Finite_element_method_in_structural_mechanics#Interpolation_or_shape_functions) and its derivatives, the assembly of the discretised stiffness matrix ([@sec:building]), the numerical solution of the system of equations ([@sec:solving]) and the computation of the gradient of the solution (@sec:stress-computation). Yet, the fact that all these a-priori unconnected steps give rise to pretty pictures that resemble reality is still astonishing to me. |
|
|
|
divert(0) |
|
|
|
|
|
|
|
|
|
|
|
Again, take all this information as coming from a fellow that has already taken such a journey from college’s pencil and paper to real engineering cases involving complex numerical calculations. And developing, in the meantime, both an actual working finite-element [back-end](https://www.seamplex.com/fino) and [front-end](https://www.caeplex.com) from scratch.^[The dean of the engineering school I attended used to say “It is not the same to read than to write manuals, and we should aim at writing them.”] |
|
|
|
Again, take all this information as coming from a fellow that has already taken such a journey from college’s pencil and paper to real engineering cases involving complex numerical calculations. And developing, in the meantime, both an actual working finite-element [back-end](https://www.seamplex.com/fino) and [front-end](https://www.caeplex.com) from scratch.dnl^[The dean of the engineering school I attended used to say “It is not the same to read than to write manuals, and we should aim at writing them.”] |
|
|
|
|
|
|
|
|
|
|
|
### Tips and tricks |
|
|
|
@@ -46,8 +52,10 @@ Again, take all this information as coming from a fellow that has already taken |
|
|
|
There are some useful tricks that come handy when trying to solve a mechanical problem. Throughout this text, I will try to tell you some of them. |
|
|
|
|
|
|
|
|
|
|
|
One of the most important ones to use your _imagination_. You will need a lot of imagination to “see” what it is actually going on when analysing an engineering problem. This skill comes from my background in nuclear engineering where I had no choice but to imagine a [positron-electron annihilation](https://en.wikipedia.org/wiki/Electron%E2%80%93positron_annihilation) or an [spontaneous fission](https://en.wikipedia.org/wiki/Spontaneous_fission). But in mechanical engineering, it is likewise important to be able to imagine how the loads “press” one element with the other, how the material reacts depending on its properties, how the nodal displacements generate stresses (both normal and shear), how results converge, etc. And what these results actually mean besides the pretty-coloured figures.^[A former boss once told me “I need the CFD” when I handed in some results. I replied that I did not do computational fluid-dynamics but computed the neutron flux kinetics within a nuclear reactor core. He joked “I know, what I need are the _Colors For Directors_, those pretty-coloured figures along with your actual results to convince the managers.”] |
|
|
|
This journey will definitely need your imagination. We will take a look at equations, numbers, plots, schematics, CAD geometries, 3D\ views, etc. Still, when the theory says “thermal expansion produces normal stresses” you have to picture in your head three little arrows pulling away from the same point in three directions, or whatever mental picture you have about what you understand thermally-induced stresses are. What comes to your mind when someone says that out of the nine elements of the [stress tensor](https://en.wikipedia.org/wiki/Cauchy_stress_tensor) ([@sec:tensor]) there are only six that are independent? Whatever it is, try to practice that kind of graphical thoughts with every new concept. Nevertheless, there will be particular locations of the text where imagination will be most useful. I will bring the subject up then and again. |
|
|
|
One of the most important ones to use your _imagination_. You will need a lot of imagination to “see” what it is actually going on when analysing an engineering problem. This skill comes from my background in nuclear engineering where I had no choice but to imagine a [positron-electron annihilation](https://en.wikipedia.org/wiki/Electron%E2%80%93positron_annihilation) or an [spontaneous fission](https://en.wikipedia.org/wiki/Spontaneous_fission). But in mechanical engineering, it is likewise important to be able to imagine how the loads “press” one element with the other, how the material reacts depending on its properties, how the nodal displacements generate stresses (both normal and shear), how results converge, etc. |
|
|
|
dnl And what these results actually mean besides the pretty-coloured figures.^[A former boss once told me “I need the CFD” when I handed in some results. I replied that I did not do computational fluid-dynamics but computed the neutron flux kinetics within a nuclear reactor core. He joked “I know, what I need are the _Colors For Directors_, those pretty-coloured figures along with your actual results to convince the managers.”] |
|
|
|
|
|
|
|
This journey will definitely need your imagination. We will peek a little bit into equations, numbers, plots, schematics, CAD geometries, 3D\ views, etc. Still, when the theory says “thermal expansion produces normal stresses” you have to picture in your head three little arrows pulling away from the same point in three directions, or whatever mental picture you have about what you understand thermally-induced stresses are. What comes to your mind when someone says that out of the nine elements of the [stress tensor](https://en.wikipedia.org/wiki/Cauchy_stress_tensor) ([@sec:tensor]) there are only six that are independent? Whatever it is, try to practice that kind of graphical thoughts with every new concept. Nevertheless, there will be particular locations of the text where imagination will be most useful. I will bring the subject up then and again. |
|
|
|
|
|
|
|
|
|
|
|
Another heads up is that we will be digging into some mathematics. Probably they would be simple and you would deal with them very easily. But chances are you do not like equations. No problem! Just ignore them for now. Read the text skipping them, it should work as well. |
|
|
|
@@ -67,13 +75,13 @@ After further years passed by, engineers (probably the same people that forked s |
|
|
|
|
|
|
|
![Three-dimensional CAD model for the piping system of\ [@fig:isometric]](real-piping.png){#fig:real-life width=75%} |
|
|
|
|
|
|
|
|
|
|
|
### Nuclear reactors |
|
|
|
|
|
|
|
In each of the countries that have at least one nuclear power plant there exists a national regulatory body who is responsible for allowing the owner to operate the reactor. These operating licenses are time-limited, with a range that can vary from 25 to 60 years, depending on the design and technology of the reactor. Once expired, the owner might be entitled to an extension, which the regulatory authority can accept provided it can be shown that a certain (and very detailed) set of safety criteria are met. One particular example of requirements is that of fatigue in pipes, especially those that belong to systems that are directly related to the reactor safety. |
|
|
|
|
|
|
|
### Pressurised pipes |
|
|
|
|
|
|
|
|
|
|
|
How come that pipes are subject to fatigue? Well, on the one hand and without getting into many technical details, the most common nuclear reactor design uses liquid water as coolant and moderator. On the other hand, nuclear power plants cannot by-pass the thermodynamics of the [Carnot cycle](https://en.wikipedia.org/wiki/Carnot_cycle), and in order to maximise the efficiency of the conversion of the energy stored in the uranium nuclei into electricity we need to reach temperatures as high as possible. So, if we want to have liquid water in the core as hot as possible, we need to increase the pressure. The limiting temperature and pressure are given by the [critical point of water](https://en.wikipedia.org/wiki/Critical_point_(thermodynamics)), which is around 374ºC and 22\ MPa. It is therefore expected to have temperatures and pressures near those values in many systems of the plant, especially in the primary circuit and those that directly interact with it, such as pressure and inventory control system, decay power removal system, feedwater supply system, emergency core-cooling system, etc. |
|
|
|
|
|
|
|
Nuclear power plants are not always working at 100% of their maximum power capacity. They need to be maintained and refuelled, they may undergo operational (and some incidental) transients, they might operate at a lower power due to load following conditions, etc. These transient cases involve changes both in temperatures and in pressures that the pipes are subject to, which in turn give rise to changes in the stresses within the pipes. As the transients are postulated to occur cyclically during a number of times during the life-time of the plant (plus its extension period), mechanical fatigue in these piping systems may arise, especially at the interfaces between materials with different thermal expansion coefficients. |
|
|
|
@@ -138,7 +146,7 @@ What does this all have to do with mechanical engineering? Well, once we know wh |
|
|
|
|
|
|
|
### An infinitely-long pressurised pipe {#sec:infinite-pipe} |
|
|
|
|
|
|
|
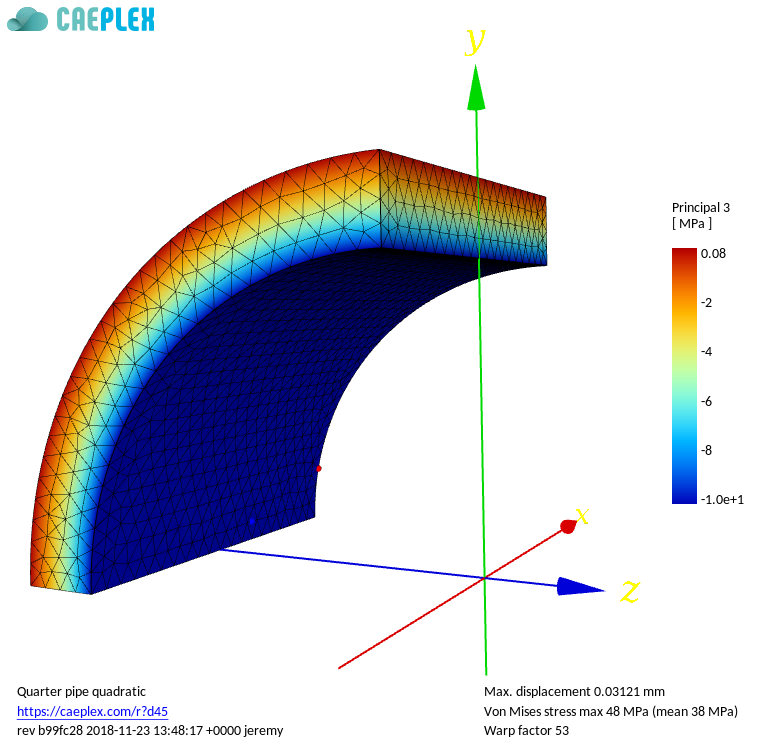
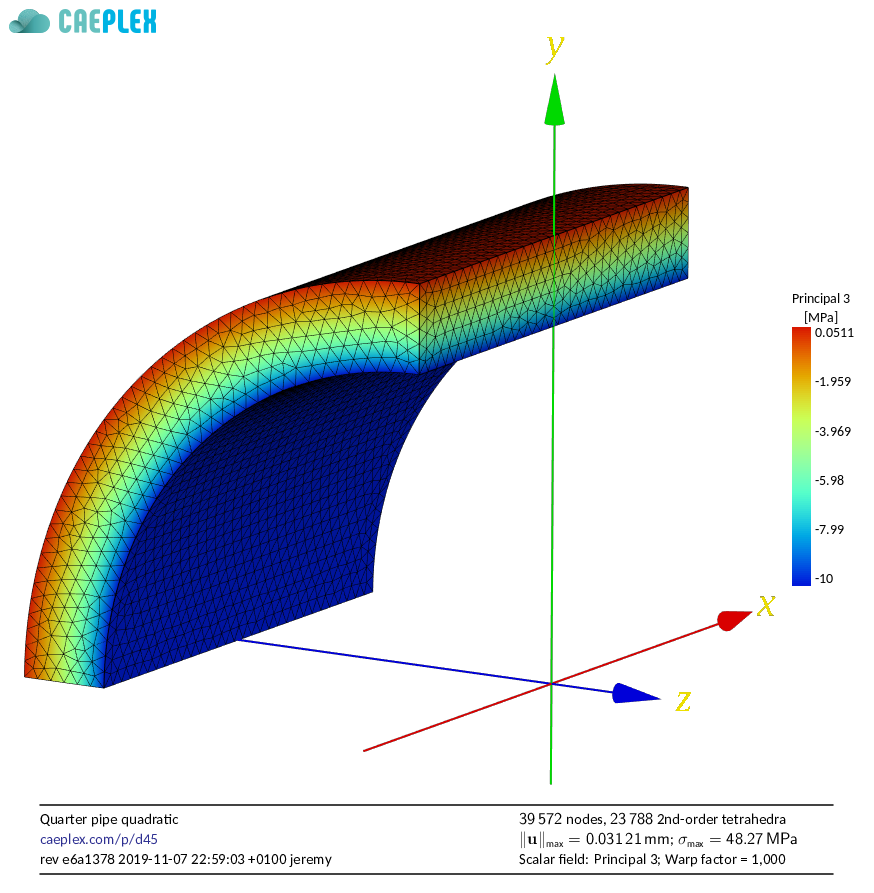
Let us proceed to our second step, and consider the infinite pipe subject to uniform internal pressure already introduced in\ [@fig:infinite-pipe]. Actually, we are going to solve the mechanical problem on an infinite hollow cylinder, which looks like pipe. This case is usually tackled in college courses, and chances are you already solved it. In fact, the first (and simpler) problem is the “thin cylinder problem.” Then, the “thick cylinder problem” is introduced (the one we solve below), which is slightly more complex. Nevertheless, it has an [analytical solution](https://www.seamplex.com/fino/doc/pipe-linearized/). For the present case, let us consider an infinite pipe (i.e. a hollow cylinder) of internal radius $a$ and external radius $b$ with uniform mechanical properties---Young’s modulus $E$ and Poisson’s ratio $\nu$---subject to an internal uniform pressure $p$. |
|
|
|
Let us proceed to our second step, and consider the infinite pipe subject to uniform internal pressure already introduced in\ [@fig:infinite-pipe]. Actually, we are going to solve the mechanical problem on an infinite hollow cylinder, which looks like pipe. This case is usually tackled in college courses, and chances are you already solved it. In fact, the first (and simpler) problem is the “thin cylinder problem.” Then, the “thick cylinder problem” is introduced (the one we solve below), which is slightly more complex. Nevertheless, it has an analytical solution.^[A detailed analysis of the analytical solution and how results obtained with finite elements converge with respect to the mesh size can be found in the report “On convergence of linearized stresses in an infinite pipe computed using the finite element method.” See [@sec:online].] For the present case, let us consider an infinite pipe (i.e. a hollow cylinder) of internal radius $a$ and external radius $b$ with uniform mechanical properties---Young’s modulus $E$ and Poisson’s ratio $\nu$---subject to an internal uniform pressure $p$. |
|
|
|
|
|
|
|
What follows is more or less what we are taught in school: some equations with a brief explanation of the results. And then we move on to the next subject. |
|
|
|
|
|
|
|
@@ -160,7 +168,7 @@ What does this mean? Well, that overall the whole pipe expands a little bit radi |
|
|
|
1. linearly with the pressure, i.e. twice the pressure means twice the displacement, and |
|
|
|
2. inversely proportional to the Young’s Modulus\ $E$ divided by $1+\nu$, i.e. the more resistant the material, the less radial displacements. |
|
|
|
|
|
|
|
That is how an infinite pipe withstands internal pressure. |
|
|
|
That is how an infinite pipe withstands internal pressure. And that is what we are taught in college, which is actually true by the way! |
|
|
|
|
|
|
|
#### Stresses |
|
|
|
|
|
|
|
@@ -333,7 +341,7 @@ Remember the main issue of the fatigue analysis in these systems is to analyse w |
|
|
|
|
|
|
|
|
|
|
|
::::: {#fig:weldolet} |
|
|
|
{#fig:weldolet-cad width=65%} |
|
|
|
{#fig:weldolet-cad width=65%} |
|
|
|
|
|
|
|
{#fig:weldolet-mesh width=85%} |
|
|
|
|
|
|
|
@@ -344,7 +352,7 @@ CAD model of a piping system with a 3/4-inch weldolet-type fork (stainless steel |
|
|
|
{#fig:weldolet-scls width=75%} |
|
|
|
|
|
|
|
|
|
|
|
On the one hand, a reasonable number of nodes (it is the number of nodes that defines the problem size, not the number of elements as discussed in [@sec:elements-nodes]) in order to get a decent grid is around 200k for each system. On the other hand, solving a couple of dozens of transient heat transfer problems (which we cannot avoid due to the large thermal inertia of the pipes) during a few thousands of seconds over a couple hundred of thousands of nodes might take more time and storage space to hold the results than we might expect. |
|
|
|
On the one hand, a reasonable number of nodes (it is the number of nodes that defines the problem size, not the number of elements) in order to get a decent grid is around 200k for each system. On the other hand, solving a couple of dozens of transient heat transfer problems (which we cannot avoid due to the large thermal inertia of the pipes) during a few thousands of seconds over a couple hundred of thousands of nodes might take more time and storage space to hold the results than we might expect. |
|
|
|
|
|
|
|
There is a wonderful essay by [Isaac Asimov](https://en.wikipedia.org/wiki/Isaac_Asimov) called [“The Relativity of Wrong”](https://en.wikipedia.org/wiki/The_Relativity_of_Wrong) where he introduces the idea that even if something cannot be computed exactly, there are different levels of error. For instance, believing that the Earth is a sphere is less wrong than believing that the Earth is flat, but wrong nonetheless, since it really deviates from a perfect sphere and resembles more an oblate spheroid. |
|
|
|
|
|
|
|
@@ -358,7 +366,7 @@ We can then merge this idea by Asimov with an adapted version of the [Saint-Vena |
|
|
|
|
|
|
|
As an example, let us consider the system depicted in\ [@fig:valve] where there is a stainless-carbon steel interface at the discharge of the valves. Instead of solving the transient heat-conduction problem with the internal temperature of the pipes equal to the temperature of the water in the reference transient condition of the power plant and an external condition of natural convection to the ambient temperature in the whole mesh, a reduced model consisting of half of one of the two valves and a small length of the pipes at both the valve inlet and outlet is used. Once the temperature distribution\ $\hat{T}(\mathbf{x},t)$ for each time is obtained in the reduced mesh ([@fig:valve-temp], which has the origin at the centre of the valve), the actual temperature distribution\ $T(\mathbf{x},t)$ is computed by an algebraic generalisation of $\hat{T}(\mathbf{x},t)$ in the full coordinate system. As stated above, those locations which are not covered by the reduced model are generalised with a time-dependent uniform temperature which is the average of the inner and outer temperatures at the inlet and outlet of the reduced mesh. |
|
|
|
|
|
|
|
{#fig:valve-temp width=80%} |
|
|
|
{#fig:valve-temp width=80%} |
|
|
|
|
|
|
|
|
|
|
|
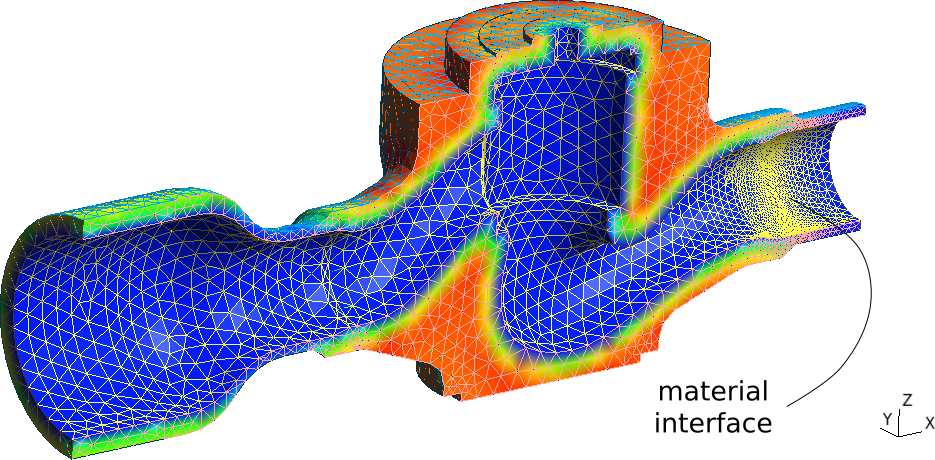
Note that there is no need to have a one-to-one correspondence between the elements from the reduced mesh with the elements from the original one. Actually, the reduced mesh contains first-order elements whilst the former has second-order elements. Also the grid density is different. Nevertheless, the finite-element solver [Fino](https://www.seamplex.com/fino) used to solve both the heat and the mechanical problems, allows to read functions of space and time defined over one mesh and continuously evaluate and use them into another one even if the two grids have different elements, orders or even dimensions. In effect, in the system from\ [@fig:real-life] the material interface is between a orifice plate made in stainless steel that is welded to a carbon-steel pipe ([@fig:real]). The thermal problem can be modelled using a two-dimensional axi-symmetric grid and then generalised to the full three-dimensional mesh using the algebraic manipulation capabilities provided by [Fino](https://www.seamplex.com/fino) (actually by [wasora](https://www.seamplex.com/wasora)) as shown in\ [@fig:real]. |
|
|
|
@@ -366,16 +374,17 @@ Note that there is no need to have a one-to-one correspondence between the eleme |
|
|
|
dnl {#fig:real-mesh2 width=70%} |
|
|
|
dnl {#fig:real-temp width=34%} |
|
|
|
|
|
|
|
{#fig:real width=85%} |
|
|
|
{#fig:real width=85%} |
|
|
|
|
|
|
|
|
|
|
|
### Seismic loads {#sec:seismic} |
|
|
|
|
|
|
|
Before considering the actual mechanical problem that will give us the stress tensor at the SCLs, and besides needing to solve the transient thermal problem to get the temperature distributions, we need to address the loads that arise due to a postulated earthquake during a certain part of the operational transients. The full computation of a mechanical transient problem using the earthquake time-dependent displacements is off the table for two reasons. First, because again the computation would take more time than we might have to deliver the report. And secondly and more importantly, because civil engineers do not compute earthquakes in the time domain but in the frequency domain using the [response spectrum method](https://en.wikipedia.org/wiki/Response_spectrum), provided the case is linear (see\ [@sec:linearity]). Time to revisit our [Fourier transform](https://en.wikipedia.org/wiki/Fourier_transform) exercises from undergraduate math courses. |
|
|
|
|
|
|
|
Every nuclear power plant is designed to withstand earthquakes. Of course, not all plants need the same level of reinforcements. Those built in large quiet plains will be, seismically speaking, cheaper than those located in geologically active zones. Keep in mind that all the 54 Japanese nuclear power plants did structurally resist the 2011 earthquake, and all of the reactors were safely shut down. What actually happened in [Fukushima](http://www.world-nuclear.org/information-library/safety-and-security/safety-of-plants/fukushima-accident.aspx) is that one hour after the main shake, a 14-metre tsunami splashed on the coast, jumping over the 9-metre defences and flooding the emergency [Diesel generators](https://en.wikipedia.org/wiki/Diesel_generator) that provided power to the pumps in charge of removing the remaining [decay power](https://en.wikipedia.org/wiki/Decay_heat) from the already-stopped [reactor core](https://en.wikipedia.org/wiki/Nuclear_reactor_core). |
|
|
|
|
|
|
|
divert(-1) |
|
|
|
#### Earthquake spectra |
|
|
|
|
|
|
|
Every nuclear power plant is designed to withstand earthquakes. Of course, not all plants need the same level of reinforcements. Those built in large quiet plains will be, seismically speaking, cheaper than those located in geologically active zones. Keep in mind that all the 54 Japanese nuclear power plants did structurally resist the 2011 earthquake, and all of the reactors were safely shut down. What actually happened in [Fukushima](http://www.world-nuclear.org/information-library/safety-and-security/safety-of-plants/fukushima-accident.aspx) is that one hour after the main shake, a 14-metre tsunami splashed on the coast, jumping over the 9-metre defences and flooding the emergency [Diesel generators](https://en.wikipedia.org/wiki/Diesel_generator) that provided power to the pumps in charge of removing the remaining [decay power](https://en.wikipedia.org/wiki/Decay_heat) from the already-stopped [reactor core](https://en.wikipedia.org/wiki/Nuclear_reactor_core). |
|
|
|
|
|
|
|
Back to our case study, the point is that each site where nuclear power plants are built must have a geological study where a postulated design-basis earthquake is to be defined. In other words, a theoretical earthquake which the plant ought to withstand needs to be specified. How? By giving a set of three spectra (one for each coordinate direction) giving acceleration as a function of the frequency for each level of the building. That is to say, once the earthquake hits the power plant, depending on soil-structure interactions the energy will shake the building foundations in a way that depends on the characteristics of the earthquake, the soil and the concrete structure. Afterwards, the way the oscillations travel upward and shake each of the mechanical components erected in each floor level depends on the design of the civil structure in a way which is fully determined by the floor response spectra like the ones depicted in\ [@fig:spectrum]. |
|
|
|
|
|
|
|
@@ -399,8 +408,13 @@ A real continuous solid has infinite modes of oscillation. A discretised one (us |
|
|
|
|
|
|
|
{#fig:acumulada} |
|
|
|
|
|
|
|
|
|
|
|
These first modes, shown in\ [@fig:modes], that take up most of the energy are then used to take into account the earthquake load. There are several ways of performing this computation, but the ASME\ III code states that the method known as SRSS (for Square Root of Sum of Squares) can be used. This method mixes the eigenvectors with the floor response spectra through the eigenvalues and gives a spatial (actually nodal) distribution of three accelerations (one for each direction) that, when multiplied by the density of the material, give a vector of a distributed force (in units of Newton per cubic millimetre for example) which is statically equivalent to the load coming from the postulated earthquake. |
|
|
|
divert(0) |
|
|
|
|
|
|
|
|
|
|
|
::::: {#fig:modes} |
|
|
|
](mode1.png){width=48%}\ |
|
|
|
](mode1-commented.png){width=48%}\ |
|
|
|
](mode2.png){width=48%} |
|
|
|
|
|
|
|
](mode3.png){width=48%}\ |
|
|
|
@@ -409,12 +423,9 @@ A real continuous solid has infinite modes of oscillation. A discretised one (us |
|
|
|
](mode5.png){width=48%}\ |
|
|
|
](mode6.png){width=48%} |
|
|
|
|
|
|
|
First six natural oscillation modes for a piping section between axial supports. Blue-red color scale shows magnitude of deformation, as compared to the original geometry (grey). Animations can be seen at links like <https://www.seamplex.com/docs/nafems4/mode1.webm>. |
|
|
|
First six natural oscillation modes for a piping section between axial supports. Blue-red colour scale shows magnitude of deformation, as compared to the original geometry (grey). Full animations available online ([@sec:online]). |
|
|
|
::::: |
|
|
|
|
|
|
|
|
|
|
|
These first modes, shown in\ [@fig:modes], that take up most of the energy are then used to take into account the earthquake load. There are several ways of performing this computation, but the ASME\ III code states that the method known as SRSS (for Square Root of Sum of Squares) can be used. This method mixes the eigenvectors with the floor response spectra through the eigenvalues and gives a spatial (actually nodal) distribution of three accelerations (one for each direction) that, when multiplied by the density of the material, give a vector of a distributed force (in units of Newton per cubic millimetre for example) which is statically equivalent to the load coming from the postulated earthquake. |
|
|
|
|
|
|
|
::::: {#fig:acceleration} |
|
|
|
{width=80%} |
|
|
|
|
|
|
|
@@ -422,10 +433,11 @@ These first modes, shown in\ [@fig:modes], that take up most of the energy are t |
|
|
|
|
|
|
|
{width=80%} |
|
|
|
|
|
|
|
The equivalent accelerations for the piping section of [@fig:modes] for the spectra of\ [@fig:spectrum] |
|
|
|
Equivalent accelerations for a certain piping section |
|
|
|
::::: |
|
|
|
|
|
|
|
The ASME code says that these accelerations (depicted in [@fig:acceleration]) ought to be applied twice: once with the original sign and once with all the elements with the opposite sign, as SRSS “looses signs.” The application of each of these equivalent loads should last two seconds in the original time domain. |
|
|
|
Since the computation of the loads that a certain earthquake gives rise to would add a significant amount of complexity to this already-complex case study, the details are skipped. In any case, we need to compute the first natural modes of oscillation of the piping section under study ([@fig:modes]) and then, after some cumbersome maths, obtain an statically-equivalent load distribution. In effect, [@fig:acceleration] shows a sample distribution of acceleration distribution within a certain piping system which, when multiplied by the density, give a load distribution which is statically equivalent to the dynamic solicitations created by the earthquake. |
|
|
|
The ASME code says that these accelerations ought to be applied twice: once with the original sign and once with all the elements with the opposite sign, as SRSS “looses signs.” The application of each of these equivalent loads should last two seconds in the original time domain. |
|
|
|
|
|
|
|
|
|
|
|
### Linearity (not yet linearisation) {#sec:linearity} |
|
|
|
@@ -436,17 +448,17 @@ Let us jump out of our nuclear piping problem and step back into the general fin |
|
|
|
|
|
|
|
\medskip |
|
|
|
|
|
|
|
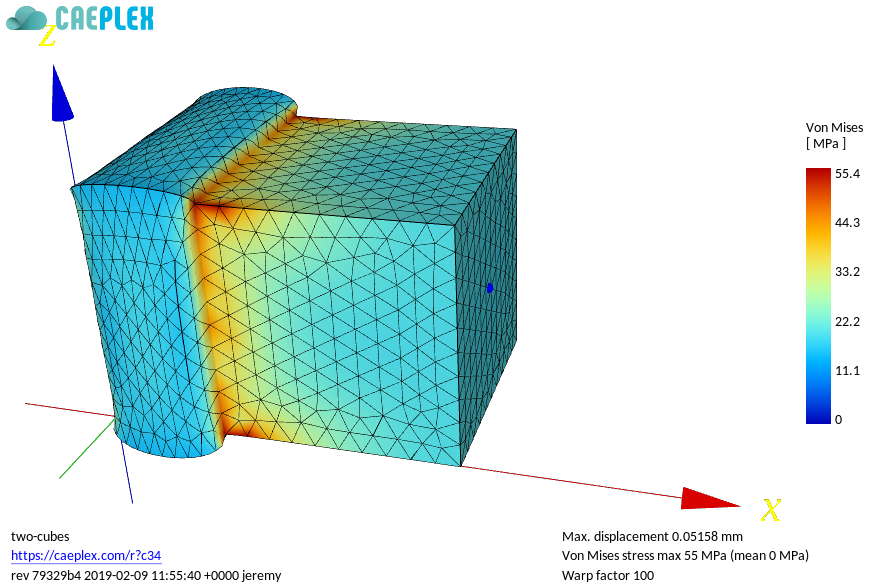
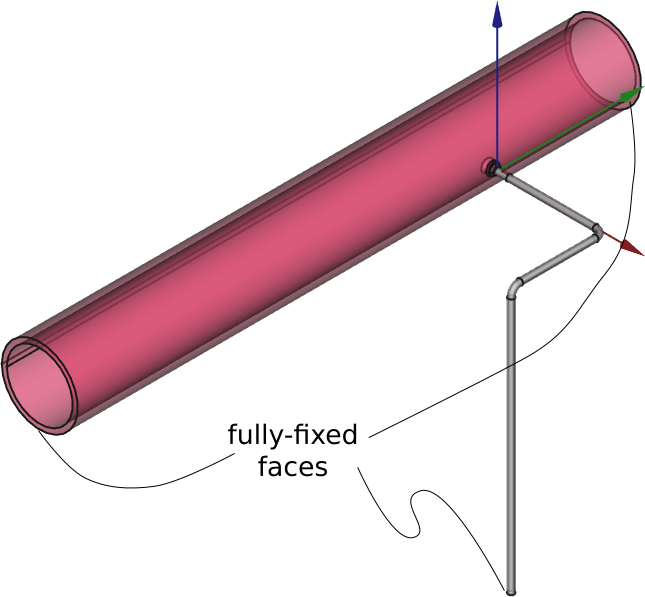
Time for both of us to make an experiment. Grab your favourite FEM program for the first time (remember mine is [CAEplex](https://caeplex.com)) and create a 1mm $\times$ 1mm $\times$ 1mm cube. Set any values for the Young’s Modulus and Poisson ratio as you want. I chose\ $E=200$\ GPa and\ $\nu=0.28$. Restrict the three faces pointing to the negative axes to their planes, i.e. |
|
|
|
Time for both of us to make an experiment. Grab your favourite FEM program for the first time (remember mine is [CAEplex](https://caeplex.com), which can also be accessed through [Onshape](https://www.onshape.com/cad-blog/partner-spotlight-using-caeplex-for-finite-element-analysis-in-onshape)) and create a 1mm $\times$ 1mm $\times$ 1mm cube. Set any values for the Young’s Modulus and Poisson ratio as you want. I chose\ $E=200$\ GPa and\ $\nu=0.28$. Restrict the three faces pointing to the negative axes to their planes, i.e. |
|
|
|
|
|
|
|
* in face “left” ($x<0$), set null displacement in the $x$ direction ($u=0$), |
|
|
|
* in face “front” ($y<0$), set null displacement in the $y$ direction ($v=0$), |
|
|
|
* in face “bottom” ($z<0$), set null displacement in the $z$ direction ($w=0$). |
|
|
|
|
|
|
|
Now we are going to create and compare three load cases: |
|
|
|
Now we are going to create and compare three load cases:^[The provided links lead to FEA cases which are fully usable directly from the web browser, i.e. “finite elements in the cloud.”] |
|
|
|
|
|
|
|
a. Pure normal loads (<https://caeplex.com/p/d8f>) |
|
|
|
a. Pure normal loads (<https://caeplex.com/p/d8fe>) |
|
|
|
b. Pure shear loads (<https://caeplex.com/p/b494>) |
|
|
|
c. The combination of A & B (<https://caeplex.com/p/989>) |
|
|
|
c. The combination of A & B (<https://caeplex.com/p/9899>) |
|
|
|
|
|
|
|
The loads in each cases are applied to the three remaining faces, namely “right” ($x>0$), “back” ($y>0$) and “top,” ($z>0$). Their magnitude in Newtons are: |
|
|
|
|
|
|
|
@@ -477,8 +489,9 @@ $$ |
|
|
|
|
|
|
|
|
|
|
|
::::: {#fig:cube} |
|
|
|
{#fig:cube-shear width=48%}\ |
|
|
|
{#fig:cube-full width=48%} |
|
|
|
{#fig:cube-shear width=65%} |
|
|
|
|
|
|
|
{#fig:cube-full width=65%} |
|
|
|
|
|
|
|
Spatial distribution of principal stress\ 3 for cases\ B and\ C. If linearity applied, case\ C would be equal to case\ B plus a constant |
|
|
|
::::: |
|
|
|
@@ -623,14 +636,14 @@ The first thing that has to be said is that, as with any interesting problem, th |
|
|
|
10. etc. |
|
|
|
|
|
|
|
::::: {#fig:quarter} |
|
|
|
{#fig:cube-struct width=48%}\ |
|
|
|
{#fig:quarter-caeplex width=48%} |
|
|
|
{#fig:cube-struct width=50%}\ |
|
|
|
{#fig:quarter-caeplex width=50%} |
|
|
|
|
|
|
|
Two of the hundreds of different ways the infinite pressurised pipe can be solved using FEM. The axial displacement at the ends is set to zero, leading to a [plane-strain](https://en.wikipedia.org/wiki/Plane_stress#Plane_strain_(strain_matrix)) condition |
|
|
|
::::: |
|
|
|
|
|
|
|
|
|
|
|
You can get both the exponential nature of each added bullet and how easily we can add new further choices to solve a FEM problem. And each of these choices will reveal you something about the nature of either the mechanical problem or the numerical solution. It is not possible to teach any possible lesson from every outcome in college, so you will have to learn them by yourself getting your hands at them. I have already tried to address the particular case of the infinite pipe in a [recent report](https://www.seamplex.com/fino/doc/pipe-linearized/)^[<https://www.seamplex.com/fino/doc/pipe-linearized/>] that is worth reading before carrying on with this article. |
|
|
|
You can get both the exponential nature of each added bullet and how easily we can add new further choices to solve a FEM problem. And each of these choices will reveal you something about the nature of either the mechanical problem or the numerical solution. It is not possible to teach any possible lesson from every outcome in college, so you will have to learn them by yourself getting your hands at them. I have already tried to address the particular case of the infinite pipe in a [recent report](https://www.seamplex.com/fino/doc/pipe-linearized/)^[The aforementioned “On convergence of linearized stresses in an infinite pipe computed using the finite element method.”] that is worth reading before carrying on with this article. |
|
|
|
The main conclusions of the report are: |
|
|
|
|
|
|
|
dnl * Engineering problems ought not to be solved using black-boxes (i.e. privative software whose source code is not freely available)---more on the subject below in\ [@sec:two-materials]. |
|
|
|
@@ -640,12 +653,12 @@ dnl * There are no shear stresses, so these three stresses are also the principa |
|
|
|
dnl * Analytical expressions for the membrane and membrane plus bending stresses along any radial SCL can be obtained. |
|
|
|
dnl * The spatial domain can be discretised using linear or higher-order elements. In particular first and second-order elements have been used in the report. |
|
|
|
* For the same number of elements, second-order grids need more nodes than linear ones, although they can better represent curved geometries. |
|
|
|
* The discretised problem size depends on the number of nodes and not on the number of elements---more on the subject below in\ [@sec:elements-nodes]. |
|
|
|
dnl * The discretised problem size depends on the number of nodes and not on the number of elements---more on the subject below in\ [@sec:elements-nodes]. |
|
|
|
dnl * The finite-element results for the displacements are similar to the analytical solution, with second-order grids giving better results for the same number of elements (this is expected as they involved far more nodes). |
|
|
|
* The three stress distributions computed with the finite-element give far more reasonable results for the second-order case than for the first-order grid. This is qualitatively explained by the fact that first-order tetrahedra have uniform derivatives and such the elements located in both the external and external faces represent the stresses not at the actual faces but at the barycentre of the elements. |
|
|
|
* Membrane stresses converge well for both the first and second-order cases because they represent a zeroth-order moment of the stress distribution and the excess and defect errors committed by the internal and external elements approximately cancel out. |
|
|
|
* Membrane plus bending stresses converge very poorly with linear elements because the excess and defect errors do not cancel out because it is a first-order moment of the stress distribution. |
|
|
|
* The computational effort to solve a given problem, namely the CPU time and the needed RAM ([@fig:error-vs-cpu]) depend non-linearly on various factors, but the most important one is the problem size which is three times the number of nodes in the grid---more on the subject below in\ [@sec:elements-nodes]. |
|
|
|
* The computational effort to solve a given problem, namely the CPU time and the needed RAM ([@fig:error-vs-cpu]) depend non-linearly on various factors, but the most important one is the problem size which is three times the number of nodes in the grid dnl---more on the subject below in\ [@sec:elements-nodes]. |
|
|
|
* The error with respect to the analytical solutions as a function of the CPU time needed to compute the membrane stress is similar for both first and second-order grids. But for the computation of the membrane plus bending stress ([@fig:error-MB-vs-cpu]), first-order grids give very poor results compared to second-order grids for the same CPU time. |
|
|
|
|
|
|
|
::::: {#fig:error-vs-cpu} |
|
|
|
@@ -657,6 +670,7 @@ Error in the computation of the linearised stresses vs. CPU time needed to solve |
|
|
|
|
|
|
|
An additional note should be added. The FEM solution, which not only gives the nodal displacements but also a method to interpolate these values inside the elements, does not fully satisfy the original equilibrium equations at every point (i.e. the strong formulation). It is an approximation to the solution of the [weak formulation](https://en.wikipedia.org/wiki/Weak_formulation) that is close (measured in the vector space spanned by the [shape functions](https://www.quora.com/What-is-a-shape-function-in-FEM)) to the real solution. Mechanically, this means that the FEM solution leads only to nodal equilibrium but not point-wise equilibrium. |
|
|
|
|
|
|
|
divert(-1) |
|
|
|
### Elements, nodes and CPU {#sec:elements-nodes} |
|
|
|
|
|
|
|
dnl The last two bullets above lead to an issue that has come many times when discussing the issue of convergence with respect to the mesh size with other colleagues. There apparently exists a common misunderstanding that the number of elements is the main parameter that defines how complex a FEM model is. This is strange, because even in college we are taught that the most important parameter is the _size_ of the stiffness matrix, which is three times (for 3D problems with the [displacement-based formulation](http://web.mit.edu/kjb/www/Books/FEP_2nd_Edition_4th_Printing.pdf) formulation) the number of _nodes_. |
|
|
|
@@ -732,7 +746,7 @@ Now proceed to picturing the general three-dimensional cases with unstructured t |
|
|
|
Detailed mathematics show that the location where the derivatives of the interpolated displacements are closer to the real (i.e. the analytical ones in problems that have it) solution are the elements’ [Gauss points](https://en.wikipedia.org/wiki/Gaussian_quadrature). Even better, the material properties at these points are continuous (they are usually uniform but they can depend on temperature for example) because, unless we are using weird elements, there are no material interfaces inside elements. But how to manage a set of stresses given at the Gauss points instead of at the nodes? Should we use one mesh for the input and another one for the output? What happens when we need to know the stresses on a surface and not just in the bulk of the solid? There are still no one-size-fits-all answers. There is a very interesting [blog post](https://nickjstevens.netlify.com/post/2019/stress-singularities/) by Nick Stevens that addresses the issue of stresses computed at sharp corners. What does your favourite FEM program do with such a case? |
|
|
|
|
|
|
|
In any case, this step takes a non-negligible amount of time. The most-common approach, i.e. the node-averaging method is driven mainly by the number of nodes of course. So all-in-all, these are the reasons to use the number of nodes instead of the numbers of elements as a basic parameter to measure the complexity of a FEM problem. |
|
|
|
|
|
|
|
divert(0) |
|
|
|
|
|
|
|
## Adding complexity: the truth is out there |
|
|
|
|
|
|
|
@@ -861,7 +875,7 @@ Do you now see the added value of training throw-ins with watermelons? We might |
|
|
|
* using distributed forces from earthquakes, |
|
|
|
* etc. |
|
|
|
|
|
|
|
Most of the time at college we would barely do what is needed to be approved in one course and move on to the next one. If you have the time and consider a career related to finite-element analysis, please do not. Clone the repository^[<https://github.com/seamplex/tee>] with the input files for [Fino](https://www.seamplex.com/fino) and start playing. If you are stuck, do not hesitate asking for help in [wasora’s mailing list](https://www.seamplex.com/lists.html). |
|
|
|
Most of the time at college we would barely do what is needed to be approved in one course and move on to the next one. If you have the time and consider a career related to finite-element analysis, please do not. Clone the repository ([@sec:online]) with the input files for [Fino](https://www.seamplex.com/fino) and start playing. If you are stuck, do not hesitate asking for help in [wasora’s mailing list](https://www.seamplex.com/lists.html). |
|
|
|
|
|
|
|
One further detail: it is always a sane check to try to explain the numerical results based on physical reasoning (i.e. “with your fingers”) as we did two paragraphs above. Most of the time you will be solving problems whilst already knowing what the result would (or ought to) be. |
|
|
|
|
|
|
|
@@ -872,7 +886,7 @@ A fellow mechanical engineer who went to the same high school I did, who went to |
|
|
|
|
|
|
|
So here we are again with the case study where we have to compute the linearised stresses at certain SCLs located near the interface between two different kinds of steels during operational and incidental transients of the plant. The first part is then to “bake” the pipes, modelling a thermal transient with time-dependent temperature or convection boundary conditions (it depends on the system). This steps gives a time and space-dependent temperature\ $T(x,y,z,t)$. |
|
|
|
|
|
|
|
Then we proceed to “shake” the pipes, i.e. to compute the natural frequencies and associated oscillations modes. Employing the floor response spectra and combining the individual contributions with the SRSS method discussed in section\ [@sec:seismic], we obtain a distributed load vector\ $\mathbf{f}(x,y,z)$ which is statically equivalent to the design earthquake. |
|
|
|
We then proceed to “shake” the pipes. That is to say, we obtain a distributed load vector\ $\mathbf{f}(x,y,z)$ which is statically equivalent to the design earthquake. |
|
|
|
|
|
|
|
Finally we attempt to “break” the pipes successively solving many steady-state elastic problems for different times\ $t$ of the operational transient. Some remarks about this step: |
|
|
|
|
|
|
|
@@ -908,7 +922,11 @@ If you notice, the complex dependence of the stiffness matrix\ $K$ can be reduce |
|
|
|
|
|
|
|
$$ K(\mathbf{x}) \cdot \mathbf{u}(\mathbf{x}) = \mathbf{b}(\mathbf{x})$$ |
|
|
|
|
|
|
|
And this last equation is linear in\ $\mathbf{u}$. In effect, the discretisation step means to integrate over\ $\mathbf{x}$. As\ $K$, $\mathbf{u}$ and\ $\mathbf{b}$ depend only on\ $\mathbf{x}$, then after integration one gets just numbers with the matrix representation of\ [@eq:kub]. Again, you can either trust me, ask a teacher or go through with the maths (in increasing order of recommendation). |
|
|
|
And this last expression is linear in\ $\mathbf{u}$! In effect, the discretisation step means to integrate over\ $\mathbf{x}$. As\ $K$, $\mathbf{u}$ and\ $\mathbf{b}$ depend only on\ $\mathbf{x}$, then after integration one gets just numbers inside $K$ and $\mathbf{b}$. Again, you can either, in increasing order of recommendation: |
|
|
|
|
|
|
|
1. trust me, |
|
|
|
2. ask a teacher, or |
|
|
|
3. go through with the maths. |
|
|
|
|
|
|
|
|
|
|
|
::::: {#fig:case} |
|
|
|
@@ -943,7 +961,7 @@ Temperature distribution for a certain instant of the transient, computed in the |
|
|
|
](case-mode9.png){#fig:case-mode-9 width=30%} |
|
|
|
|
|
|
|
First nine natural modes of oscillation of the piping system subject to the boundary conditions the supports provide. |
|
|
|
Animations can be seen at links like <https://www.seamplex.com/docs/nafems4/case-mode1.webm>. |
|
|
|
Animations are available online ([@sec:online]). |
|
|
|
::::: |
|
|
|
|
|
|
|
dnl {#fig:case-spectrum width=70%} |
|
|
|
@@ -955,15 +973,15 @@ To recapitulate, the figures in this section show some partial non-dimensional r |
|
|
|
3. defining the number and locations of the SCLs ([@fig:case-scls] or [@fig:weldolet-scls;@fig:valve]) |
|
|
|
4. computing a heat conduction (bake) transient problem with temperatures as a function of time from the operational transient in a simple domain using temperature-dependent thermal conduction coefficients from ASME\ II\ part D ([@fig:case-temp] or [@fig:valve-temp]) |
|
|
|
5. generalising the temperature distribution as a function of time to the general domain ([@fig:case-temp2] or [@fig:real]) |
|
|
|
6. performing a modal analysis (shake) on the main domain to obtain the main oscillation frequencies and modes ([@fig:case-mode] or [@fig:modes]) |
|
|
|
7. using the floor response spectra ([@fig:spectrum]) and the SRSS method to obtain a distributed force statically-equivalent to the earthquake load ([@fig:case-acceleration] or [@fig:acceleration]) |
|
|
|
6. performing a modal analysis (shake) on the main domain to obtain the main oscillation frequencies and modes ([@fig:case-mode] dnl or [@fig:modes]) |
|
|
|
7. obtaining a distributed force statically-equivalent to the earthquake load (shake, [@fig:case-acceleration] or [@fig:acceleration]) |
|
|
|
8. successively solving the linear elastic problem for different times using the generalised temperature distribution taking into account |
|
|
|
a. the dependence of the Young’s Modulus\ $E$ and the thermal expansion coefficient\ $\alpha$ with temperature, |
|
|
|
b. the thermal expansion effect itself |
|
|
|
c. the instantaneous pressure exerted in the internal faces of the pipes at the time\ $t$ according to the definition of the operational transient |
|
|
|
d. the restriction of the degrees of freedom of those faces, lines or points that correspond to mechanical supports located both within and at the ends of the CAD model |
|
|
|
e. the earthquake load, which according to ASME should be present only during four seconds of the transient: two seconds with one sign and the other two seconds with the opposite sign. This period should be selected to coincide with the instant of highest mechanical stress (conservative computation) |
|
|
|
9. computing the linearised stresses (membrane and membrane plus bending) at the SCLs combining them as Principal\ 1, Principal\ 2, Principal\ 3 and Tresca |
|
|
|
9. computing the linearised stresses (membrane and membrane plus bending) at the SCLs combining them as Principal\ 1, Principal\ 2, Principal\ 3 and Tresca^[A deep technical note should be added for discussing the validity of linearising a stress invariant as the principall stresses individually. It should be enough for the present study to keep in mind that in [@sec:in-air] it is the difference of these linearised principal stresses (i.e. Tresca-like) are used to compute the stress amplitude of the periodic load for fatigue assessment.] |
|
|
|
10. juxtaposing these linearised stresses for each time of the transient and for each transient so as to obtain a single time-history of stresses including all the operational and/or incidental transients under study, which is what stress-based fatigue assessment needs (recall\ [@sec:fatigue] and go on to\ [@sec:usage]). |
|
|
|
|
|
|
|
A pretty nice list of steps, which definitely I would not have been able to tackle when I was in college. Would you? |
|
|
|
@@ -1009,7 +1027,8 @@ When\ $\text{CUF} < 1$, then the part under analysis can withstand the proposed |
|
|
|
This cryptic paragraph can be better explained by using a clearer example. To avoid using actual sensitive data from a real power plant, let us use the same test case used by both the [US Nuclear Regulatory Commission](https://en.wikipedia.org/wiki/Nuclear_Regulatory_Commission) (in its report NUREG/CR-6909) and the [Electric Power Institute](https://en.wikipedia.org/wiki/Electric_Power_Research_Institute) (report 1025823) called “EAF (Environmentally-Assisted Fatigue) Sample Problem 2-Rev.\ 2 (10/21/2011)”. |
|
|
|
|
|
|
|
|
|
|
|
{#fig:axi-inches-3d width=25%} |
|
|
|
{#fig:axi-inches-3d width=35%} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
It consists of a typical vessel nozzle with attached piping as illustrated in\ [@fig:axi-inches-3d]. These components are subject to four transients\ $k=1,2,3,4$ that give rise to linearised stress histories (slightly modified according to NB-3216.2) which are given as individual stress values juxtaposed so as to span a time range of about 36,000 seconds ([@fig:nureg1]). As the time steps is not constant, each stress value has an integer index\ $i$ that uniquely identifies it: |
|
|
|
@@ -1021,8 +1040,24 @@ It consists of a typical vessel nozzle with attached piping as illustrated in\ [ |
|
|
|
| 3 | 6450--9970 | 960--1595 | 20 | |
|
|
|
| 4 | 9970--35971 | 1596--2215 | 100 | |
|
|
|
|
|
|
|
A design-basis earthquake was assumed to occur briefly during one second (sic) at around\ $t=3470$\ seconds, and it is assigned a number of cycles\ $n_e=5$. The detailed stress history for one of the SCLs including both the principal and lineariased stresses, which are already offset following NB-3216.2 so as to have a maximum stress equal to zero, can be found as an appendix in NRC's NUREG/CR-6909 report, or in the repository with the scripts I prepared for you to play with this problem.^[<https://github.com/seamplex/cufen>] |
|
|
|
|
|
|
|
A design-basis earthquake was assumed to occur briefly during one second (sic) at around\ $t=3470$\ seconds, and it is assigned a number of cycles\ $n_e=5$. The detailed stress history for one of the SCLs including both the principal and lineariased stresses, which are already offset following NB-3216.2 so as to have a maximum stress equal to zero, can be found as an appendix in NRC's NUREG/CR-6909 report, or in the repository with the scripts I prepared for you to play with this problem. |
|
|
|
|
|
|
|
To compute the global usage factor, we first need to find all the combinations of local extrema pairs and then sort them in decreasing order of stress difference. For example, the largest stress amplitude is found between $i=447$ and $i=694$. The second one is 447--699. Then 699--1020, 699--899, etc. For each of these pairs, defined by the indexes\ $i_{1,j}$ and $i_{2,j}$, a partial usage factor\ $U_j$ should computed. The stress amplitude\ $S_{\text{alt},j}$ which should be used to enter into the $S$-$N$ curve is |
|
|
|
|
|
|
|
\pagebreak |
|
|
|
|
|
|
|
|
|
|
|
$$ |
|
|
|
S_{\text{alt},j} = \frac{1}{2} \cdot k_{e,j} \cdot \left| MB^\prime_{i_{1,j}} - MB^\prime_{i_{2,j}} \right| \cdot \frac{E_\text{SN}}{E(T_{\text{max}_j})} |
|
|
|
$$ |
|
|
|
|
|
|
|
\noindent where $k_e$ is a plastic correction factor for large loads (NB-3228.5), $E_\text{SN}$ is the Young’s Modulus used to create the $S$-$N$ curve (provided in the ASME fatigue curves) and\ $E(T_{\text{max}_j})$ is the material’s Young’s Modulus at the maximum temperature within the\ $j$-th interval. |
|
|
|
|
|
|
|
|
|
|
|
We now need to comply with ASME’s obscure note about the number of cycles to assign a proper value of\ $n_j$. Back to the largest pair 447-694, we see that 447 belongs to transient\ #1 which has assigned 20 cycles and 694 belongs to the earthquake with 5 cycles. Therefore $n_1=5$, and the cycles associated to each index are decreased in five. So $i=694$ disappears and the number of cycles associated to $i=447$ are decreased from 20 to 15. The second largest pair is now 447-699, with 15 (because we just spent 5 in the first pair) and 50 cycles respectively. Now $n_2=15$, point 447 disappears and 699 remains with 35 cycles. The next pair is 699-1020, with number of cycles 35 and 20 so $n_3=20$, point 1020 disappears and 699 remains with 15 cycles. And so on, down to the last pair. |
|
|
|
|
|
|
|
Why all these details? Not because I want to teach you how to perform fatigue evaluations just reading this section without resorting to ASME, fatigue books and even other colleagues. It is to show that even though these computation can be made “by hand” (i.e. using a calculator or, God forbids, a spreadsheet) when having to evaluate a few SCLs within several piping systems it is far (and I mean really far) better to automate all these steps by writing a set of scripts. Not only will the time needed to process the information be reduced, but also the introduction of human errors will be minimised and repeatability of results will be assured---especially if working under a [distributed version control](https://en.wikipedia.org/wiki/Distributed_version_control) system such as [Git](https://en.wikipedia.org/wiki/Git). This is true in general, so here is another tip: learn to write scripts to post-process your FEM results (you will need to use a script-friendly FEM program) and you will gain considerable margins regarding time and quality. |
|
|
|
|
|
|
|
::::: {#fig:nureg} |
|
|
|
{#fig:nureg1 width=70%} |
|
|
|
@@ -1034,14 +1069,6 @@ A design-basis earthquake was assumed to occur briefly during one second (sic) a |
|
|
|
Time history of the linearised stress\ $\text{MB}_{31}$ corresponding to the example problem from NRC and EPRI. The indexes\ $i$ of the extrema are shown in green (minimums) and red (maximums) |
|
|
|
::::: |
|
|
|
|
|
|
|
|
|
|
|
To compute the global usage factor, we first need to find all the combinations of local extrema pairs and then sort them in decreasing order of stress difference. For example, the largest stress amplitude is found between $i=447$ and $i=694$. The second one is 447--699. Then 699--1020, 699--899, etc. For each of these pairs, defined by the indexes\ $i_{1,j}$ and $i_{2,j}$, a partial usage factor\ $U_j$ should computed. The stress amplitude\ $S_{\text{alt},j}$ which should be used to enter into the $S$-$N$ curve is |
|
|
|
|
|
|
|
$$ |
|
|
|
S_{\text{alt},j} = \frac{1}{2} \cdot k_{e,j} \cdot \left| MB^\prime_{i_{1,j}} - MB^\prime_{i_{2,j}} \right| \cdot \frac{E_\text{SN}}{E(T_{\text{max}_j})} |
|
|
|
$$ |
|
|
|
where $k_e$ is a plastic correction factor for large loads (NB-3228.5), $E_\text{SN}$ is the Young’s Modulus used to create the $S$-$N$ curve (provided in the ASME fatigue curves) and\ $E(T_{\text{max}_j})$ is the material’s Young’s Modulus at the maximum temperature within the\ $j$-th interval. |
|
|
|
|
|
|
|
::::: {#fig:cuf} |
|
|
|
{#fig:cuf-nrc width=100%} |
|
|
|
|
|
|
|
@@ -1050,9 +1077,6 @@ where $k_e$ is a plastic correction factor for large loads (NB-3228.5), $E_\text |
|
|
|
Tables of individual usage factors for the NRC/EPRI “EAF Sample Problem 2-Rev.\ 2 (10/21/2011).” One table is taken from a document issued by almost-a-billion-dollar-year-budget government agency from the most powerful country in the world and the other one is from a third-world engineering startup. Guess which is which. |
|
|
|
::::: |
|
|
|
|
|
|
|
We now need to comply with ASME’s obscure note about the number of cycles to assign a proper value of\ $n_j$. Back to the largest pair 447-694, we see that 447 belongs to transient\ #1 which has assigned 20 cycles and 694 belongs to the earthquake with 5 cycles. Therefore\ $n_1=5$, and the cycles associated to each index are decreased in five. So $i=694$ disappears and the number of cycles associated to $i=447$ are decreased from 20 to 15. The second largest pair is now 447-699, with 15 (because we just spent 5 in the first pair) and 50 cycles respectively. Now $n_2=15$, point\ 447 disappears and 699 remains with 35 cycles. The next pair is 699-1020, with number of cycles 35 and 20 so $n_3=20$, point 1020 disappears and 699 remains with 15 cycles. And so on, down to the last pair. |
|
|
|
|
|
|
|
Why all these details? Not because I want to teach you how to perform fatigue evaluations just reading this section without resorting to ASME, fatigue books and even other colleagues. It is to show that even though these computation can be made “by hand” (i.e. using a calculator or, God forbids, a spreadsheet) when having to evaluate a few SCLs within several piping systems it is far (and I mean really far) better to automate all these steps by writing a set of scripts. Not only will the time needed to process the information be reduced, but also the introduction of human errors will be minimised and repeatability of results will be assured---especially if working under a [distributed version control](https://en.wikipedia.org/wiki/Distributed_version_control) system such as [Git](https://en.wikipedia.org/wiki/Git). This is true in general, so here is another tip: learn to write scripts to post-process your FEM results (you will need to use a script-friendly FEM program) and you will gain considerable margins regarding time and quality. |
|
|
|
|
|
|
|
### In water (NRC’s extension) {#sec:in-water} |
|
|
|
|
|
|
|
@@ -1096,7 +1120,7 @@ Tables of individual environmental correction and usage factors for the NRC/EPRI |
|
|
|
|
|
|
|
## Conclusions |
|
|
|
|
|
|
|
Back in college, we all learned how to solve engineering problems. And once we graduated, we felt we could solve and fix the world (if you did not graduate yet, you will feel it shortly). But there is a real gap between the equations written in chalk on a blackboard (now probably in the form of beamer slide presentations) and actual real-life engineering problems. This chapter introduces a real case from the nuclear industry and starts by idealising the structure such that it has a known analytical solution that can be found in textbooks. Additional realism is added in stages allowing the engineer to develop an understanding of the more complex physics and a faith in the veracity of the finite-element results where theoretical solutions are not available. Even more, a brief insight into the world of evaluation of stress-life fatigue using such results further illustrates the complexities of real-life engineering analysis. Here is a list of the tips that arose throughout the text: |
|
|
|
Back in college, we all learned how to solve engineering problems. And once we graduated, we felt we could solve and fix the world (if you did not graduate yet, you will feel it shortly). But there is a real gap between the equations written in chalk on a blackboard (now probably in the form of beamer slide presentations) and actual real-life engineering problems. This chapter introduces a real case from the nuclear industry and starts by idealising the structure such that it has a known analytical solution that can be found in textbooks. Additional realism is added in stages allowing the engineer to develop an understanding of the more complex physics and a faith in the veracity of the finite-element results where theoretical solutions are not available. Even more, a brief insight into the world of evaluation of stress-life fatigue using such results further illustrates the complexities of real-life engineering analysis, even though the presented case was simplified for the sake of clearness. Here is a list of the tips that arose throughout the text: |
|
|
|
|
|
|
|
* use and exercise your imagination |
|
|
|
* practise math |
|
|
|
@@ -1105,29 +1129,28 @@ Back in college, we all learned how to solve engineering problems. And once we g |
|
|
|
* remember there are other methods beside finite elements |
|
|
|
* take into account that even within the finite element method, there is a wide variety of complexity in the problems that can be solved |
|
|
|
dnl * follow the “five whys rule” before compute anything, probably you do not need to |
|
|
|
* use engineering judgment and make sure understand Asimov’s [“wronger than wrong”](https://en.wikipedia.org/wiki/Wronger_than_wrong) concept |
|
|
|
dnl * use engineering judgement and make sure understand Asimov’s [“wronger than wrong”](https://en.wikipedia.org/wiki/Wronger_than_wrong) concept |
|
|
|
* play with your favourite FEM solver (mine is [CAEplex](https://caeplex.com)) solving simple cases, trying to predict the results and picturing the stress tensor and its eigenvectors in your imagination |
|
|
|
* prove (with pencil and paper) that even though the principal stresses are not linear with respect to summation, they are linear with respect to multiplication |
|
|
|
* grab any stress distribution from any of your FEM projects, compute the iso-stress curves and the draw normal lines to them to get acquainted with SCLs |
|
|
|
* search online for “stress linearisation” (or “linearization” if you want) and then get a copy of ASME\ VIII Div\ 2 Annex 5-A |
|
|
|
* take into account that FEM solutions lead only to nodal equilibrium but not point-wise equilibrium |
|
|
|
* measure the time needed to generate grids of different sizes and kinds with your favourite mesher |
|
|
|
* learn this by heart: the complexity of a FEM problem is given mainly by the number of _nodes_, not by the number of elements |
|
|
|
dnl * measure the time needed to generate grids of different sizes and kinds with your favourite mesher |
|
|
|
dnl * learn this by heart: the complexity of a FEM problem is given mainly by the number of _nodes_, not by the number of elements |
|
|
|
* remember that welded materials with different thermal expansion coefficients may lead to fatigue under cyclic temperature changes |
|
|
|
dnl * if you have time, try to get out of your comfort zone and do more than what others expect from you (like parametric computations) |
|
|
|
* clone the [parametric tee repository](https://github.com/seamplex/tee), understand how the figures from\ [@sec:parametric] were built and expand them to cover “we might go on...” bullets |
|
|
|
* try to find an explanation of the results obtained, just like we did when we explained the parametric curves from\ [@fig:tee-MB ] with two opposing effects which were equal in magnitude around $d_b=5$\ inches |
|
|
|
* think thermal-mechanical plus earthquakes as “bake, break and shake” problems |
|
|
|
* think thermal-mechanical plus earthquakes cases as “bake, break and shake” problems |
|
|
|
* understand why the elastic problem of the case study is still linear after all |
|
|
|
* keep in mind that finite-elements are a means to get an engineering solution, not an end by themselves |
|
|
|
* learn to write scripts to post-process FEM results (from a script-friendly FEM program) |
|
|
|
* learn to write scripts to post-process FEM results (from an script-friendly open-source FEM program) |
|
|
|
* work under a [distributed version control](https://en.wikipedia.org/wiki/Distributed_version_control) system such as [Git](https://en.wikipedia.org/wiki/Git), even when just editing input files or writing reports |
|
|
|
dnl * clone the [environmental fatigue sample problem repository](https://bitbucket.org/seamplex/cufen) and obtain a nicely-formatted table with the results of the “EAF Sample Problem 2-Rev.\ 2 (10/21/2011)” from\ [@sec:in-air;@sec:in-water]. |
|
|
|
* do not write ambiguous reports by replacing appropriate mathematical formulae with words just not to offend the illiterate |
|
|
|
* try to avoid [proprietary](https://en.wikipedia.org/wiki/Proprietary_software) programs and favour [free and open source](https://en.wikipedia.org/wiki/Free_and_open-source_software) ones. |
|
|
|
|
|
|
|
dnl You can ask for help in our mailing list at <wasora@seamplex.com>. There is a community of engineers willing to help you in case you get in trouble with the repositories, the script or the input files. |
|
|
|
|
|
|
|
|
|
|
|
About your favourite FEM program, ask yourself these two questions: |
|
|
|
|
|
|
|
1. Does your favourite FEM program’s manual say what the program does? |
|
|
|
@@ -1137,5 +1160,32 @@ About your favourite FEM program, ask yourself these two questions: |
|
|
|
|
|
|
|
And finally, make sure that at the end of the journey from college theory to an actual engineering problem your conscience is clear knowing that there exists a report with your signature on it. That is why we all went to college in the first place. |
|
|
|
|
|
|
|
### Online stuff {#sec:online} |
|
|
|
|
|
|
|
Here is a list of sub-problems and stuff to play with. |
|
|
|
|
|
|
|
* The pendulum-swing video from [@sec:intro] |
|
|
|
- <https://youtu.be/Q-lKK4A2OzA> |
|
|
|
* “On convergence of linearized stresses in an infinite pipe computed using the finite element method” from [@sec:infinite-pipe;@sec:linearity;@sec:infinite-pipe;@sec:infinite-pipe-fem] |
|
|
|
- <https://www.seamplex.com/fino/doc/pipe-linearized/> |
|
|
|
* The three cubes from [@sec:linearity] |
|
|
|
- case A: pure normal loads (<https://caeplex.com/p/d8fe>) |
|
|
|
- case B: pure shear loads (<https://caeplex.com/p/b494>) |
|
|
|
- case C: the combination of A & B (<https://caeplex.com/p/9899>) |
|
|
|
* The animations of natural oscillations in [@fig:modes] |
|
|
|
- <https://www.seamplex.com/docs/nafems4/mode1.webm> |
|
|
|
- <https://www.seamplex.com/docs/nafems4/mode2.webm> |
|
|
|
- ... |
|
|
|
* The animations of natural oscillations in [@fig:case-mode] |
|
|
|
- <https://www.seamplex.com/docs/nafems4/case-mode1.webm> |
|
|
|
- <https://www.seamplex.com/docs/nafems4/case-mode2.webm> |
|
|
|
- ... |
|
|
|
* The parametric tee repository from [@sec:parametric] |
|
|
|
- <https://github.com/seamplex/tee> |
|
|
|
* The environmental fatigue sample problem repository from [@sec:in-air;@sec:in-water] |
|
|
|
- <https://github.com/seamplex/cufen> |
|
|
|
|
|
|
|
See <https://www.seamplex.com/nafems> for new material, updated links and the full version of this case with many more details about the case and the associated mathematics. |
|
|
|
|
|
|
|
|
|
|
|
# Concluding Remarks |