gtheler
/
nafems4
Следить 1
В избранное 0
Форкнуть 0
Код Задачи 0 Pull Request'ы 0 Релизы 0 Вики Активность
Просмотр исходного кода

cosas

tags/CANDIDATE
gtheler 7 лет назад
Родитель
2216e66e1b
Сommit
b3be9c912d
15 измененных файлов: 1196 добавлений и 27 удалений
Разделённый вид Показать статистику Diff
  1. Двоичные данные
      12D-24-isometrico1.jpg
  2. +502
    -0
      fino.tex
  3. +15
    -9
      infinite-pipe.svg
  4. Двоичные данные
      isometric.jpg
  5. +66
    -0
      isometric.svg
  6. +42
    -18
      nafems4.md
  7. Двоичные данные
      original_1_0.png
  8. Двоичные данные
      original_1_1.png
  9. +2
    -0
      simple.tex
  10. +146
    -0
      syntax.tex
  11. Двоичные данные
      tee-geo1.png
  12. Двоичные данные
      tee-geo2.png
  13. Двоичные данные
      tee-scls1.png
  14. Двоичные данные
      tee-scls2.png
  15. +423
    -0
      wasora.tex

Двоичные данные
12D-24-isometrico1.jpg Просмотреть файл

Before After
Width: 5137  |  Height: 3689  |  Size: 3.7MB

+ 502
- 0
fino.tex Просмотреть файл

@@ -0,0 +1,502 @@
\lstdefinelanguage{fino}{
morekeywords={
FINO_PROBLEM,
BAKE,
HEAT,
SHAKE,
MODAL,
BREAK,
ELASTIC,
HEAT_AXISYMMETRIC,
PLANE_STRESS,
PLANE_STRAIN,
ELASTIC_AXISYMMETRIC,
DIMENSIONS,
DEGREES,
SYMMETRY_AXIS,
MESH,
N_EIGEN,
SOLUTION,
SOLUTIONS,
SOLUTION_NAMES,
UNKNOWNS,
UNKNOWN,
FINO_SOLVER,
ROUTINE,
KSP_TYPE,
PC_TYPE,
SET_NEAR_NULLSPACE,
SET_NEAR_NULL_SPACE,
DO_NOT_SET_BLOCK_SIZE,
SET_BLOCK_SIZE,
GRADIENT_EVALUATION,
GRADIENT_JACOBIAN_THRESHOLD,
PROGRESS_ASCII,
SHMEM_PROGRESS_BUILD,
PROGRESS_BUILD_SHMEM,
SHMEM_PROGRESS_SOLVE,
PROGRESS_SOLVE_SHMEM,
SHMEM_MEMORY,
MEMORY_USAGE_SHMEM,
FINO_STEP,
JUST_BUILD,
JUST_SOLVE,
DUMP_FILE_PATH,
FINO_LINEARIZE,
PHYSICAL_ENTITY,
START_POINT,
END_POINT,
FILE,
FILE_PATH,
TOTAL,
M,
MB,
PEAK,
FINO_DEBUG,
MATRICES_ASCII,
MATRICES_ASCII_STRUCTURE,
MATRICES_PETSC_BINARY,
MATRICES_PETSC_COMPRESSED_BINARY,
MATRICES_PETSC_ASCII,
MATRICES_PETSC_OCTAVE,
MATRICES_PETSC_DENSE,
MATRICES_X,
MATRICES_SNG,
MATRICES_SNG_STRUCT,
MATRICES_SIZE,
MATRICES_X_SIZE,
MATRICES_STRIDE,
INCLUDE_INPUT,
LOAD_PLUGIN,
DEFAULT_ARGUMENT_VALUE,
INCLUDE,
FROM,
TO,
ABORT,
IMPLICIT,
DO_NOT_EVALUATE_AT_PARSE_TIME,
TIME_PATH,
INITIAL_CONDITIONS_MODE,
LOAD_ROUTINE,
VAR,
CONST,
ALIAS,
IS,
AS,
VECTOR,
SIZE,
DATA,
FUNCTION_DATA,
MATRIX,
ROWS,
COLS,
FUNCTION,
NODES,
CELLS,
VECTOR_DATA,
VECTORS,
COLUMNS,
INTERPOLATION,
INTERPOLATION_THRESHOLD,
SHEPARD_RADIUS,
SHEPARD_EXPONENT,
SIZES,
X_INCREASES_FIRST,
OUTPUT_FILE,
INPUT_FILE,
MODE,
INPUT,
OUTPUT,
OPEN,
DO_NOT_OPEN,
CLOSE,
IF,
ELSE,
ENDIF,
SEMAPHORE,
SEM,
READ,
WRITE,
SHM,
SHM_OBJECT,
ASCII_FILE_PATH,
BINARY_FILE_PATH,
ASCII_FILE,
BINARY_FILE,
IGNORE_NULL,
PRINT,
NONEWLINE,
SEP,
SEPARATOR,
NOSEP,
HEADER,
STRING,
TEXT,
PRINT_FUNCTION,
MIN,
MAX,
STEP,
NSTEPS,
FORMAT,
PRINT_VECTOR,
VERTICAL,
HORIZONTAL,
ELEMS_PER_LINE,
SOLVE,
RESIDUALS,
GUESS,
METHOD,
EPSABS,
EPSREL,
MAX_ITER,
VERBOSE,
M4,
INPUT_FILE_PATH,
OUTPUT_FILE_PATH,
MACRO,
SHELL,
CALL,
HISTORY,
PARAMETRIC,
TYPE,
OUTER_STEPS,
MAX_DAUGHTERS,
OFFSET,
ADIABATIC,
FIT,
VIA,
GRADIENT,
RANGE_MIN,
RANGE_MAX,
DELTAEPSREL,
DELTAEPSABS,
DO_NOT_RERUN,
NORERUN,
RERUN,
MINIMIZE,
OPTIMIZE,
SIMAN_EFUNC,
ALGORITHM,
PHASE_SPACE,
DIFFERENTIAL,
NAME,
STRUCTURED,
ORDERING,
SCALE_FACTOR,
OFFSET_X,
OFFSET_Y,
OFFSET_Z,
NCELLS_X,
NCELLS_Y,
NCELLS_Z,
LENGTH_X,
LENGTH_Y,
LENGTH_Z,
DELTA_X,
DELTA_Y,
DELTA_Z,
READ_DATA,
READ_FUNCTION,
MESH_MAIN,
MESH_POST,
NOMESH,
NO_MESH,
NO_PHYSICAL_NAMES,
MESH_INTEGRATE,
EXPRESSION,
EXPR,
OVER,
RESULT,
GAUSS_POINTS,
MESH_FILL_VECTOR,
MESH_FIND_MAX,
I_MAX,
INDEX,
X_MAX,
Y_MAX,
Z_MAX,
ID,
MATERIAL,
BOUNDARY,
BC,
INCREMENTAL,
PHYSICAL_PROPERTY,
NONE,
ALLOWED,
AS_PROVIDED,
FROM_VARIABLES,
FROM_DERIVATIVES,
WAIT,
POST,
SKIP_STEP,
SKIP_STATIC_STEP,
SKIP_TIME,
SKIP_HEADER_STEP,
MAX_ITER,
TOL,
GRADTOL,
},
morekeywords={[2]
},
morekeywords={[3]
available_memory,
available_memory_0,
cells,
cells_0,
displ_max,
displ_max_0,
displ_max_x,
displ_max_x_0,
displ_max_y,
displ_max_y_0,
displ_max_z,
displ_max_z_0,
done,
done_0,
done_outer,
done_outer_0,
done_static,
done_static_0,
done_transient,
done_transient_0,
dont_quit,
dont_quit_0,
dont_report,
dont_report_0,
dt,
dt_0,
elements,
elements_0,
end_time,
end_time_0,
eps,
eps_0,
fino_abstol,
fino_abstol_0,
fino_dirichlet_diagonal,
fino_dirichlet_diagonal_0,
fino_divtol,
fino_divtol_0,
fino_gamg_threshold,
fino_gamg_threshold_0,
fino_iterations,
fino_iterations_0,
fino_max_iterations,
fino_max_iterations_0,
fino_penalty_weight,
fino_penalty_weight_0,
fino_reltol,
fino_reltol_0,
fino_residual_norm,
fino_residual_norm_0,
flops_petsc,
flops_petsc_0,
i,
i_0,
infinite,
infinite_0,
in_outer_initial,
in_outer_initial_0,
in_static,
in_static_0,
in_static_first,
in_static_first_0,
in_static_last,
in_static_last_0,
in_transient,
in_transient_0,
in_transient_first,
in_transient_first_0,
in_transient_last,
in_transient_last_0,
j,
j_0,
lambda,
lambda_0,
max_dt,
max_dt_0,
memory_usage_global,
memory_usage_global_0,
memory_usage_petsc,
memory_usage_petsc_0,
min_dt,
min_dt_0,
ncores,
ncores_0,
nodes,
nodes_0,
nx,
nx_0,
ny,
ny_0,
nz,
nz_0,
on_gsl_error,
on_gsl_error_0,
on_ida_error,
on_ida_error_0,
on_nan,
on_nan_0,
pi,
pi_0,
pid,
pid_0,
quit,
quit_0,
realtime_scale,
realtime_scale_0,
rel_error,
rel_error_0,
report,
report_0,
sigma_max,
sigma_max_0,
sigma_max_x,
sigma_max_x_0,
sigma_max_y,
sigma_max_y_0,
sigma_max_z,
sigma_max_z_0,
static_steps,
static_steps_0,
step_inner,
step_inner_0,
step_outer,
step_outer_0,
step_static,
step_static_0,
step_transient,
step_transient_0,
t,
t_0,
time_cpu_build,
time_cpu_build_0,
time_cpu_solve,
time_cpu_solve_0,
time_cpu_stress,
time_cpu_stress_0,
time_cpu_total,
time_cpu_total_0,
time_petsc_build,
time_petsc_build_0,
time_petsc_solve,
time_petsc_solve_0,
time_petsc_stress,
time_petsc_stress_0,
time_petsc_total,
time_petsc_total_0,
time_wall_build,
time_wall_build_0,
time_wall_solve,
time_wall_solve_0,
time_wall_stress,
time_wall_stress_0,
time_wall_total,
time_wall_total_0,
T_max,
T_max_0,
T_min,
T_min_0,
U,
U_0,
u_at_displ_max,
u_at_displ_max_0,
u_at_sigma_max,
u_at_sigma_max_0,
V,
V_0,
v_at_displ_max,
v_at_displ_max_0,
v_at_sigma_max,
v_at_sigma_max_0,
W,
W_0,
w_at_displ_max,
w_at_displ_max_0,
w_at_sigma_max,
w_at_sigma_max_0,
x,
x_0,
y,
y_0,
z,
z_0,
zero,
zero_0,
},
morekeywords={[4]
abs,
acos,
asin,
atan,
atan2,
builtindecl.h,
ceil,
clock,
cos,
cosh,
d_dt,
deadband,
derivative,
equal,
exp,
expint1,
expint2,
expint3,
expintn,
floor,
func_min,
gauss_kronrod,
gauss_legendre,
heaviside,
if,
integral,
integral_dt,
integral_euler_dt,
is_even,
is_in_interval,
is_odd,
j0,
lag,
lag_bilinear,
lag_euler,
last,
limit,
limit_dt,
log,
mark_max,
mark_min,
max,
min,
mod,
not,
prod,
random,
random_gauss,
root,
round,
sawtooth_wave,
sgn,
sin,
sinh,
sqrt,
square_wave,
sum,
tan,
tanh,
threshold_max,
threshold_min,
triangular_wave,
vecdot,
vecmax,
vecmaxindex,
vecmin,
vecminindex,
vecnorm,
vecsize,
vecsum,
},
sensitive=true,
morecomment=[l]{\#},
morestring=[b]\",
}

+ 15
- 9
infinite-pipe.svg Просмотреть файл

@@ -10,9 +10,9 @@
xmlns="http://www.w3.org/2000/svg"
xmlns:sodipodi="http://sodipodi.sourceforge.net/DTD/sodipodi-0.dtd"
xmlns:inkscape="http://www.inkscape.org/namespaces/inkscape"
width="45.098995mm"
height="42.533333mm"
viewBox="0 0 45.098995 42.533332"
width="63.693775mm"
height="61.047947mm"
viewBox="0 0 63.693775 61.047946"
version="1.1"
id="svg8"
inkscape:version="0.92.1 r15371"
@@ -24,9 +24,9 @@
borderopacity="1.0"
inkscape:pageopacity="0.0"
inkscape:pageshadow="2"
inkscape:zoom="2.8284271"
inkscape:cx="-42.674779"
inkscape:cy="67.755708"
inkscape:zoom="2"
inkscape:cx="92.733478"
inkscape:cy="109.37544"
inkscape:document-units="mm"
inkscape:current-layer="layer1"
showgrid="true"
@@ -42,8 +42,8 @@
<inkscape:grid
id="grid4487"
type="xygrid"
originx="-58.108335"
originy="-228.76458" />
originx="-58.111445"
originy="-228.76769" />
</sodipodi:namedview>
<defs
id="defs2">
@@ -685,7 +685,13 @@
id="layer1"
inkscape:groupmode="layer"
inkscape:label="Layer 1"
transform="translate(-58.108336,-25.702078)">
transform="translate(-58.111445,-7.1843505)">
<path
style="fill:#91909a;fill-opacity:1;stroke:#000000;stroke-width:0.26458332px;stroke-linecap:butt;stroke-linejoin:miter;stroke-opacity:1"
d="m 68.791667,34.533324 c 0,0 16.904676,-17.570534 22.225001,-20.902083 7.227578,-5.5736761 6.945104,0.954878 11.641662,3.704166 3.44337,1.866299 4.85454,0.610648 7.67292,3.175 2.81837,2.564353 1.13499,4.282603 2.11667,7.14375 1.53206,3.951451 1.58368,3.715782 1.32291,6.085417 -0.26077,2.369635 -20.372912,24.870834 -20.372912,24.870834 z"
id="path4855"
inkscape:connector-curvature="0"
sodipodi:nodetypes="ccczczcc" />
<circle
style="opacity:1;fill:#91909a;fill-opacity:1;stroke:#000000;stroke-width:0.30000001;stroke-miterlimit:4;stroke-dasharray:none;stroke-dashoffset:0;stroke-opacity:1"
id="circle4491"

Двоичные данные
isometric.jpg Просмотреть файл

Before After
Width: 3267  |  Height: 2057  |  Size: 1.3MB

+ 66
- 0
isometric.svg
Разница между файлами не показана из-за своего большого размера
Просмотреть файл


+ 42
- 18
nafems4.md Просмотреть файл

@@ -12,13 +12,12 @@ A simple pendulum from college physics courses and a real-life pendulum. Hint: t
:::::

::::: {#fig:pipes}
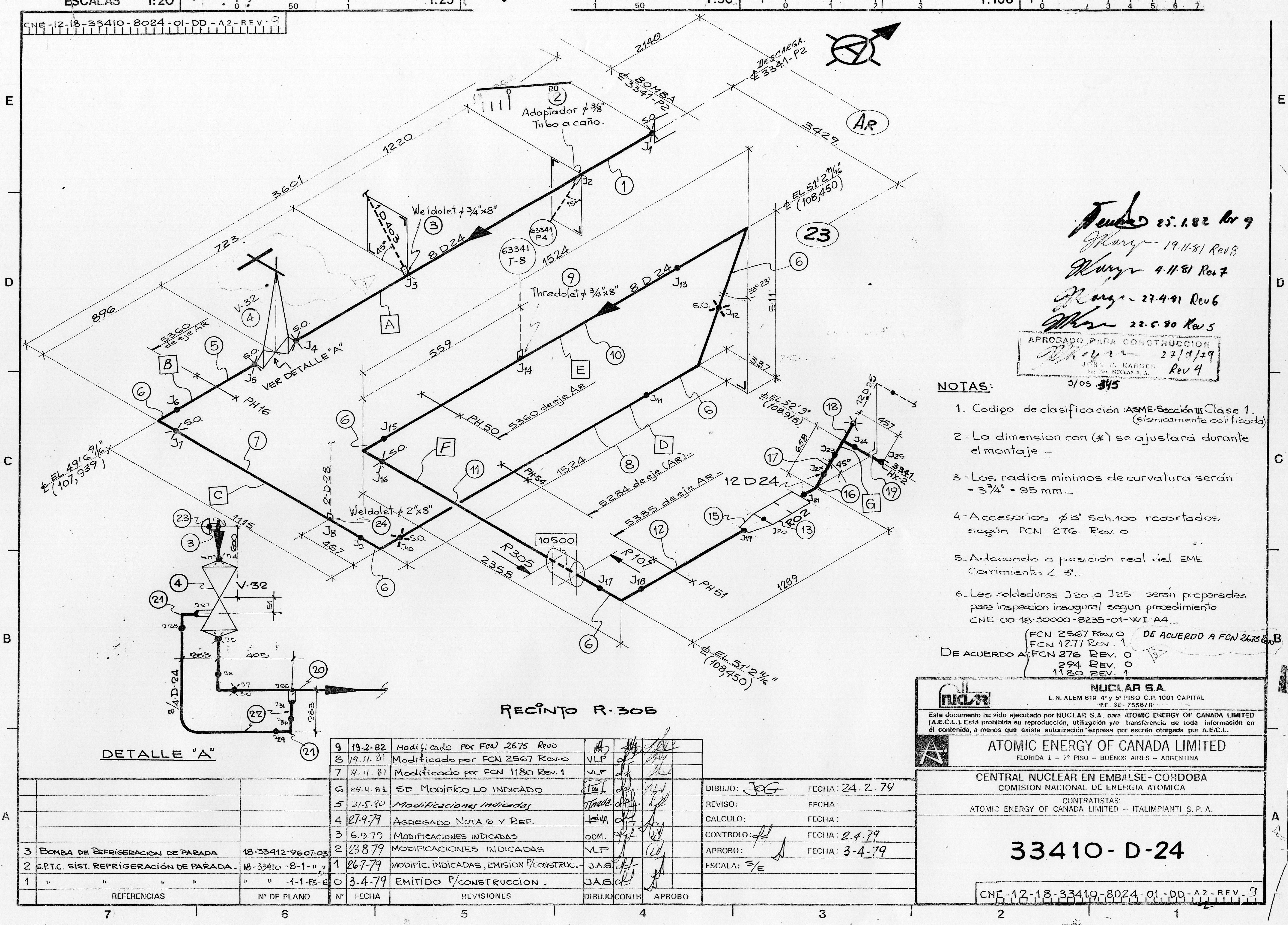
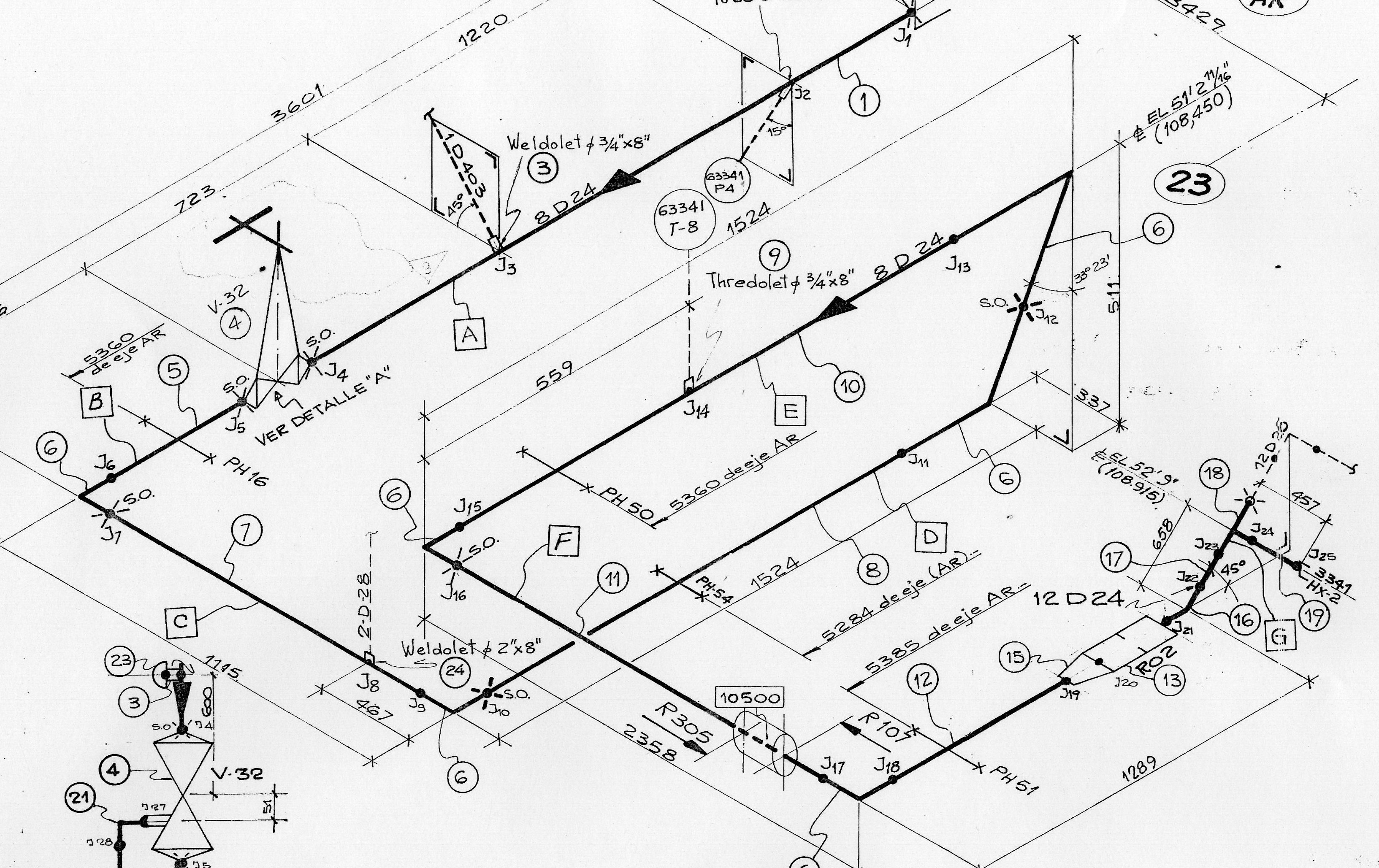
![College pipe](infinite-pipe.svg){#fig:infinite-pipe width=25%}\
![Real-life pipes](real-piping.png){#fig:real-life width=70%}
![College pipe](infinite-pipe.svg){#fig:infinite-pipe width=40%}
![Real-life pipe](isometric.svg){#fig:isometric width=58%}

An infinitely-long pressurised thick pipe as taught in college and a section of real-life piping system.
An infinitely-long pressurised thick pipe as taught in college and an isometric drawing of a section of a real-life piping system.
:::::


Whether you are a student or a seasoned engineer with many years of experience, you might recall from first year physics courses the introduction of the [simple pendulum](https://en.wikipedia.org/wiki/Pendulum) as case study\ ([@fig:simple]). You learned that the period does not depend on the hanging mass because the weight and the inertia exactly cancelled each other. Also, that Galileo said (and [Newton proved](https://www.seamplex.com/wasora/realbook/real-012-mechanics.html)) that for small oscillations the period does not even depend on the amplitude. Someone showed you why it worked this way: because if\ $\sin \theta \approx \theta$ then the motion equations converge to an [harmonic oscillator](https://en.wikipedia.org/wiki/Harmonic_oscillator). It might have been a difficult subject for you back in those days when you were learning physics and calculus at the same time. You might later study the [Lagrangian](https://en.wikipedia.org/wiki/Lagrangian_mechanics) and even the [Hamiltonian](https://en.wikipedia.org/wiki/Hamiltonian_mechanics) formulations, added a [parametric excitation](https://en.wikipedia.org/wiki/Parametric_oscillator) and studied the [chaotic double pendulum](https://www.seamplex.com/wasora/realbook/real-017-double-pendulum.html). But it was probably after college, say when you took your first son to a swing on a windy day\ ([@fig:hamaca]), that you were faced with a real pendulum worth your full attention. Ok, this is my personal story but could easily be yours as well. My point is that the very same distance between what I imagined as a student what studying a pendulum was and what I saw that day at the swing (namely that the period does depend on the hanging mass) is the same distance between the mechanical problems studied in college and the actual cases encountered during a professional engineer’s lifetime. In this regard, I am referring only to technical issues. The part of dealing with clients, colleagues, bosses, etc. which is definitely not taught in engineering schools (you can get a heads up in business schools, but again it would be a theoretical pendulum) is way beyond the scope of both this article and my own capacities.

Like the pendulums above, we will be swinging back and forth between a case study about fatigue analysis in piping systems of a nuclear power plant and more generic and even romantic topics related to finite elements and computational mechanics. These latter regressions will not remain just as abstract theoretical ideas. Not only will they be directly applicable to the development of the main case, but they will also apply to a great deal of other engineering problems tackled with the finite element method.
@@ -43,7 +42,7 @@ But, eventually, a time will come in which it cannot (or should not) be avoided.

So here comes another experience tip: do not fear equations. Even more, keep exercising. You have used differences of squares in high school. You know (or at least knew) how to integrate by parts. Remember what Laplace transforms are used for? Once in a while, perform a division of polynomials using [Ruffini’s rule](https://en.wikipedia.org/wiki/Ruffini's_rule). Or compute the second derivative of the quotient of two functions. Whatever. It should be like doing crosswords on the newspaper. Grab those old physics college books and read the exercises at the end of each chapter. It will pay off later on.

Throught the text I will be referring to “your favourite FEM program.” I bet you do have one. We will be using it to perform some tests and play a little bit. And we will use it to think about what it means to use a FEM program to generate results that will eventually end up in a written project with your signature. Keep that in mind.
Throughout the text I will be referring to “your favourite FEM program.” I bet you do have one. Mine is [CAEplex](https://caeplex.com) (it works on top of [Fino](https://www.seamplex.com/fino)). We will be using it to perform some tests and play a little bit. And we will also use it to think about what it means to use a FEM program to generate results that will eventually end up in a written project with your signature. Keep that in mind.


# Case study: nuclear reactors, pressurised pipes and fatigue {#sec:case}
@@ -57,12 +56,15 @@ After further years passed by, engineers (probably the same people that forked s

Actually, this article does not focus on a single case study but on some general ideas regarding analysis of fatigue in piping systems in nuclear power plants. There is no single case study but a compendium of ideas obtained by studying many different systems which are directly related to the safety of a real nuclear reactor.

![CAD model for the piping system of fig\ [@fig:isometric]](real-piping.png){#fig:real-life}

## Nuclear reactors

In each of the countries that have at least one nuclear power plant there exists a national regulatory body who is responsible for allowing the owner to operate the reactor. These operating licenses are time-limited, with a range that can vary from 25 to 60 years, depending on the design and technology of the reactor. Once expired, the owner might be entitled to an extension, which the regulatory authority can accept provided it can be shown that a certain (and very detailed) set of safety criteria are met. One particular example of requirements is that of fatigue in pipes, especially those that belong to systems that are directly related to the reactor safety.

## Pressurised pipes


How come that pipes are subject to fatigue? Well, on the one hand and without getting into many technical details, the most common nuclear reactor design uses liquid water as coolant and moderator. On the other hand, nuclear power plants cannot by-pass the thermodynamics of the Carnot cycle, and in order to maximise the efficiency of the conversion between the energy stored in the uranium nuclei into electricity they need to reach temperatures as high as possible. So, if we want to have liquid water in the core as hot as possible, we need to increase the pressure. The limiting temperature and pressure are given by the [critical point of water](https://en.wikipedia.org/wiki/Critical_point_(thermodynamics)), which is around 374ºC and 22\ MPa. It is therefore expected to have temperature and pressures near those values in many systems of the plant, especially in the primary circuit those that directly interact with it, such as pressure and inventory control system, decay power removal system, feedwater supply system, emergency core-cooling system, etc.

Nuclear power plants are not always working at 100% power. They need to be maintained and refuelled, they may undergo operational transients, they might operates at a lower power due to load following conditions, etc. These transient cases involved changes both in temperatures and in pressures that the pipes are subject to, which in turn give rise to changes in the stresses within the pipes. As the transients are postulated to occur conservatively cyclically during a number of times during the life-time of the plant (plus its extension period), mechanical fatigue in these piping systems arise especially at the interfaces between materials with different thermal expansion coefficients.
@@ -503,7 +505,7 @@ Even though we did not yet discuss it in detail, we want to solve an elastic pro

Let us jump out of our nuclear piping problem and step back into the general finite-element theory ground for a moment (remember we were going to jump back and forth). Assume you want to know how much your dog weights. One thing you can do is weight yourself (let us say you weight 81.2\ kg), then grab your dog and weight yourself and your dog (let us say you and your dog weight 87.3\ kg). Do you swear your dog weights 6.1\ kg plus/minus the scale’s uncertainty? I can tell you that the weight of two individual protons and two individual neutrons in not the same as the weight of an\ [$\alpha$ particle](Alpha_particle). Will not there be a master-pet interaction that renders the weighting problem non-linear?

Let us both (i.e. you and me) make an experiment. Grab a FEM program of your choice (mine is [CAEplex](https://caeplex.com)) and load a 1mm $\times$ 1mm $\times$ 1mm cube. Set any values for the Young Modulus and Poisson ratio as you want. I chose\ $E=200$MPa and\ $\nu=0.28$. Restrict the three faces pointing to the negative axes to their planes, i.e.
Let us both (i.e. you and me) make an experiment. Grab your favourite FEM programfor the first time (remember mine is [CAEplex](https://caeplex.com)) and load a 1mm $\times$ 1mm $\times$ 1mm cube. Set any values for the Young Modulus and Poisson ratio as you want. I chose\ $E=200$MPa and\ $\nu=0.28$. Restrict the three faces pointing to the negative axes to their planes, i.e.

* in face “left” ($x<0$), set null displacement in the $x$ direction ($u=0$),
* in face “front” ($y<0$), set null displacement in the $y$ direction ($v=0$),
@@ -622,7 +624,7 @@ Recall that principal stresses are the eigenvalues of the stress tensor. And the

First, let us create a 3 $\times$ 3 random matrix $R$ and then multiply it by its transpose\ $R^T$ to obtain a symmetric matrix\ $A$ (recall that the stress tensor from [@sec:tensor] is symmetric):

```octave
```{.octave style=octave}
octave> R = rand(3); A = R*R'
A =

@@ -633,7 +635,7 @@ A =

Do the same to obtain another 3 $\times$ 3 symmetric matrix\ B:

```octave
```{.octave style=octave}
octave> R = rand(3); B = R*R'
B =

@@ -644,7 +646,7 @@ B =

Now compute the sum of the eigenvalues first and then the eigenvalues of the sum:

```octave
```{.octave style=octave}
octave> eig(A)+eig(B)
ans =

@@ -873,24 +875,46 @@ Time for another experiment. We know (more or less) what to expect from an infin
So here comes the five Feynmann-Ohno questions:

1. Why do you want to perform a parametric computation?
So we can study how the linearised stresses change with the inclusion of a branch of a certain diameter.
So we can study how the linearised stresses change with the inclusion of a branch of a certain diameter (and because [we can](https://www.youtube.com/watch?v=BVd-rYIqSy8), using the `PARAMETRIC` [keyword]((https://www.seamplex.com/wasora/reference.html#parametric)) in [Fino](https://www.seamplex.com/fino)).

2. Why do you want to know how the stresses change with the inclusion of a branch?
Because it is like training throw-ins with watermelons during the week so you can reach the area with a regular ball on the weekends (football joke).
2. Why do you want to know how the stresses change with the inclusion of a branch?
Because, if we have the time, it is worth to do something harder than originally asked (football joke: it is like training throw-ins with watermelons during the week so you can reach the area with a regular ball on the weekends).

3. Why do you want to do something harder?
Because [we can](https://www.youtube.com/watch?v=BVd-rYIqSy8), and getting out of our comfort zone once in a while is a healthy habit.
Because getting out of our comfort zone once in a while is a healthy habit.

4. Why is getting out of our comfort zone a healthy habit?
Because it fires up a certain part of our brains that keep us active and allow us to better understand what is it that is going on with the problem we are solving.

5. Why do you want to understand what is going on?
For the same reason you are now reading this chapter.

4. Why is getting out of our comfort zone a healthy habit?
Because it fires up a certain part of our brains that keep us active and prevents deseases so we can live longer.

5. Why do you want to live longer?
To perform more parametric finite-element analysis.
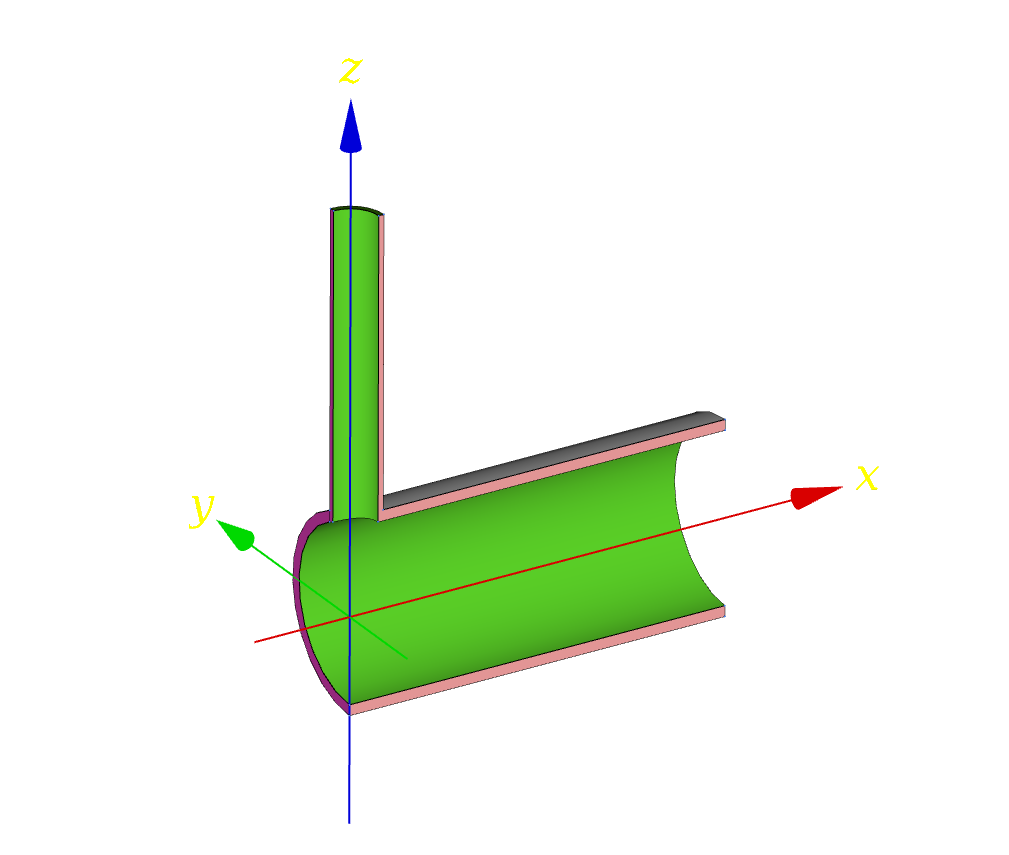
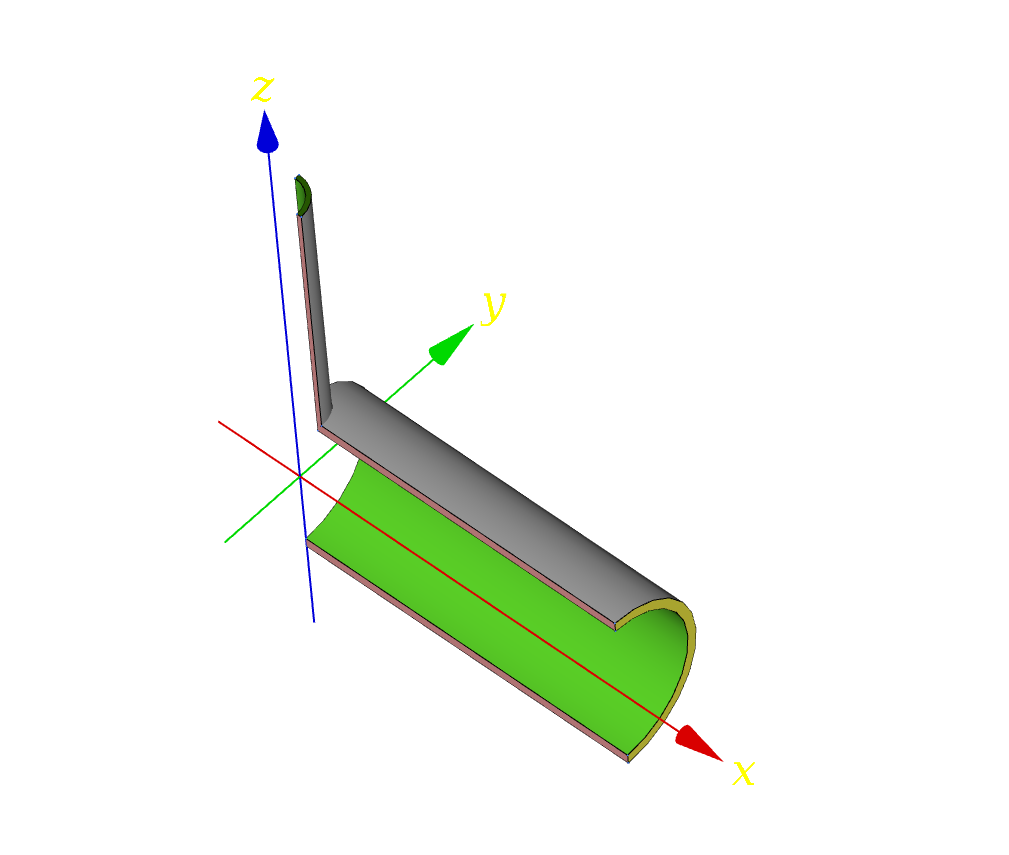
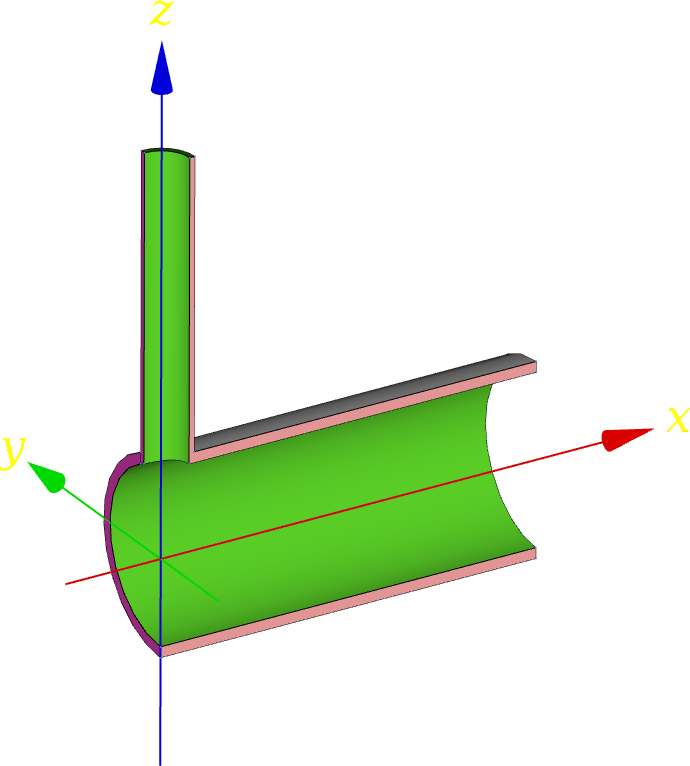
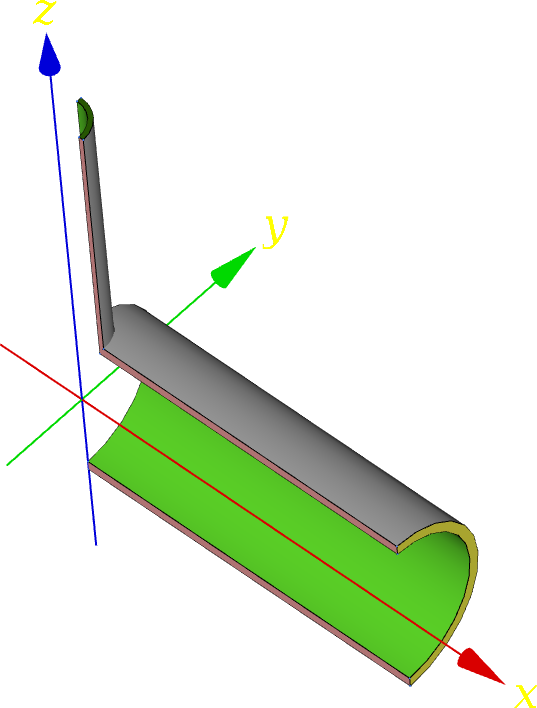
Let us solve the following mock-up case: a long main 12-inch schedule\ 80 pipe has an orthogonal branch of a certain nominal diameter of\ $d_b$\ inches (it seems that the [SI](https://en.wikipedia.org/wiki/International_System_of_Units) did not do well amongst the piping engineering community). Both the main line and the branch are pressurised with\ $p=10$\ MPa. The main pipe is aligned with the\ $x$ axis and the branch coincides with the\ $z$ axis. Thus, the $x$-$z$ plane acts as a symmetry plane and we only need to model one octant of the full geometry, as shown in\ [@fig:tee-geo]. Note that the tee is modelled as the boolean intersection of two cylinders. There are no filleted edges nor rounded corners or any other smoothing. A real CAD file containing the appropriate geometry needs to be built for the real case study.

::::: {#fig:tee-geo}
![](tee-geo1.png){#fig:tee-geo1 width=54%}\
![](tee-geo2.png){#fig:tee-geo2 width=44%}\

Let us solve the following mock-up case: a long main 12-inch schedule\ 80 pipe has an orthogonal branch of a certain nominal diameter of\ $d_b$\ inches (it seems that the [SI](https://en.wikipedia.org/wiki/International_System_of_Units) did not do well amongst the piping engineering community). Both the main line and the branch are pressurised with\ $p=10$\ MPa. The main pipe is aligned with the\ $x$ axis and the branch coincides with the\ $z$ axis. Thus, the $x$-$z$ plane acts as a symmetry plane and we only need to model one octant of the full geometry.
Geometry of the parametric 12-inch tee for the particular case of a 4-inch branch.
:::::

The boundary conditions are

* Magenta: axial symmetry $u=0$
* Salmon: plane symmetry $v=0$
* Yellow: axial $u=0$ and radial symmetry $0=vz-wy$
* Dark green: axial $w=0$ and radial symmetry $0=vx-uy$
* Light green: internal pressure\ $p=10$\ MPa

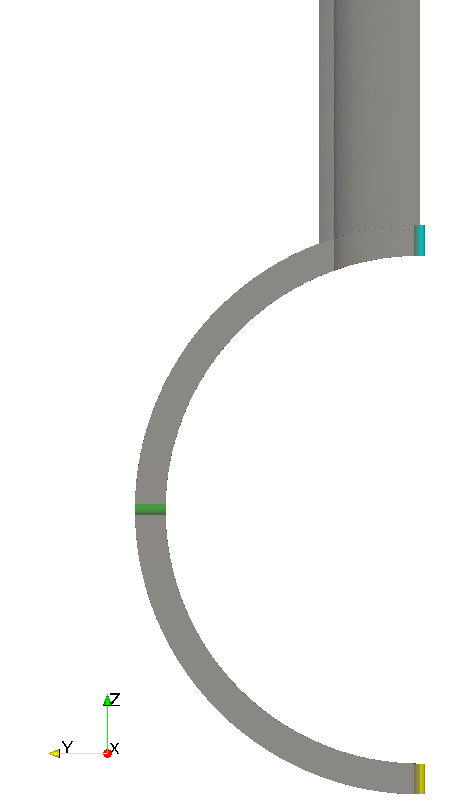
Three radial SCLs are located at a distance of one thickness of the main line from the external wall of the branch into the main direction\ $x$.

::::: {#fig:tee-scls}
![$y$-$z$ projection](tee-scls1.png){#fig:tee-scls1 width=29%}\
![$x$-$z$ projection](tee-scls2.png){#fig:tee-scls2 width=67%}\

Location of the three radial SCLs: cyan, yellow and green.
:::::

## Bake, shake and break {#sec:break}


Двоичные данные
original_1_0.png Просмотреть файл

Before After
Width: 1009  |  Height: 855  |  Size: 34KB

Двоичные данные
original_1_1.png Просмотреть файл

Before After
Width: 1009  |  Height: 855  |  Size: 39KB

+ 2
- 0
simple.tex Просмотреть файл

@@ -296,6 +296,8 @@ $if(institute)$
$endif$
\date{$date$}

\include{syntax}

\begin{document}
% \thispagestyle{empty}
% \thispagestyle{plain}

+ 146
- 0
syntax.tex Просмотреть файл

@@ -0,0 +1,146 @@
\input{wasora}
\input{fino}

\definecolor{was_keyword1}{rgb}{0.0,0.0,0.4}
\definecolor{was_keyword2}{rgb}{0.0,0.2,0.0}
\definecolor{was_variable}{rgb}{0.5,0.2,0.2}
\definecolor{was_function}{rgb}{0.2,0.5,0.2}
\definecolor{was_comment}{rgb}{0.5,0.5,0.5}

\definecolor{bash_keyword1}{rgb}{0.2,0.2,0.2}
\definecolor{bash_keyword2}{rgb}{0.7,0.7,0.7}
\definecolor{bash_comment}{rgb}{0.5,0.5,0.5}

\definecolor{was_fondo}{rgb}{0.95,0.95,0.90}
\definecolor{fino_fondo}{rgb}{0.95,0.90,0.95}
\definecolor{octave_fondo}{rgb}{0.90,0.95,0.90}
\definecolor{gmsh_fondo}{rgb}{0.90,0.90,0.95}
\definecolor{terminal_fondo}{rgb}{0.95,0.95,0.95}
\definecolor{bash_fondo}{rgb}{0.90,0.90,0.90}

% \newcommand{\MyHookSign}{\hbox{\ensuremath{\hookleftarrow}}}

\lstdefinestyle{wasora}{
language=wasora,
basicstyle=\ttfamily\footnotesize,
commentstyle={\color{was_comment}\normalfont\textit},
keywordstyle=[1]{\color{was_keyword1}\ttfamily\textbf},
keywordstyle=[2]{\color{was_keyword2}\ttfamily\textbf},
keywordstyle=[3]{\color{was_variable}\textit},
keywordstyle=[4]{\color{was_function}\textbf},
backgroundcolor=\color{was_fondo},
showstringspaces=true,
breaklines=true,
breakatwhitespace=true,
% prebreak={\space\MyHookSign},
lineskip=-1pt,
captionpos=b,
% numbers=left,
% stepnumber=5,
xleftmargin=0.2cm,
xrightmargin=0.4cm,
framesep=0.1cm,
frame=single,
}

\lstdefinestyle{fino}{
language=wasora,
basicstyle=\ttfamily\footnotesize,
commentstyle={\color{was_comment}\normalfont\textit},
keywordstyle=[1]{\color{was_keyword1}\ttfamily\textbf},
keywordstyle=[2]{\color{was_keyword2}\ttfamily\textbf},
backgroundcolor=\color{fino_fondo},
showstringspaces=true,
breaklines=true,
breakatwhitespace=true,
% prebreak={\space\MyHookSign},
lineskip=-1pt,
captionpos=b,
% numbers=left,
% stepnumber=5,
xleftmargin=0.2cm,
xrightmargin=0.4cm,
framesep=0.1cm,
frame=single,
}


\lstdefinestyle{bash}{
language=bash,
basicstyle=\ttfamily\footnotesize,
commentstyle={\color{bash_comment}\normalfont\textit},
keywordstyle=[1]{\color{bash_keyword1}\ttfamily\textbf},
keywordstyle=[2]{\color{bash_keyword2}\ttfamily\textbf},
backgroundcolor=\color{bash_fondo},
showstringspaces=true,
breaklines=true,
breakatwhitespace=true,
% prebreak={\space\MyHookSign},
lineskip=-1pt,
captionpos=b,
% numbers=left,
% stepnumber=5,
xleftmargin=0.2cm,
xrightmargin=0.2cm,
framesep=0.2cm,
frame=single,
}


\lstdefinestyle{terminal}{
language=,
basicstyle=\ttfamily\footnotesize,
backgroundcolor=\color{terminal_fondo},
breaklines=true,
% prebreak={\space\MyHookSign},
xleftmargin=0.2cm,
xrightmargin=0.2cm,
framesep=0.2cm,
frame=single,
}

\lstdefinestyle{gmsh}{
language=C,
basicstyle=\ttfamily\footnotesize,
commentstyle={\color{was_comment}\normalfont\textit},
keywordstyle=[1]{\color{was_keyword1}\ttfamily\textbf},
keywordstyle=[2]{\color{was_keyword2}\ttfamily\textbf},
keywordstyle=[3]{\color{was_variable}\textit},
keywordstyle=[4]{\color{was_function}\textbf},
backgroundcolor=\color{gmsh_fondo},
showstringspaces=true,
breaklines=true,
breakatwhitespace=true,
% prebreak={\space\MyHookSign},
lineskip=-1pt,
captionpos=b,
% numbers=left,
% stepnumber=5,
xleftmargin=0.2cm,
xrightmargin=0.4cm,
framesep=0.1cm,
frame=single,
}

\lstdefinestyle{octave}{
language=octave,
basicstyle=\ttfamily\footnotesize,
commentstyle={\color{was_comment}\normalfont\textit},
keywordstyle=[1]{\color{was_keyword1}\ttfamily\textbf},
keywordstyle=[2]{\color{was_keyword2}\ttfamily\textbf},
keywordstyle=[3]{\color{was_variable}\textit},
keywordstyle=[4]{\color{was_function}\textbf},
backgroundcolor=\color{octave_fondo},
showstringspaces=true,
breaklines=true,
breakatwhitespace=true,
% prebreak={\space\MyHookSign},
lineskip=-1pt,
captionpos=b,
% numbers=left,
% stepnumber=5,
xleftmargin=0.2cm,
xrightmargin=0.4cm,
framesep=0.1cm,
frame=single,
}

Двоичные данные
tee-geo1.png Просмотреть файл

Before After
Width: 690  |  Height: 766  |  Size: 31KB

Двоичные данные
tee-geo2.png Просмотреть файл

Before After
Width: 537  |  Height: 708  |  Size: 34KB

Двоичные данные
tee-scls1.png Просмотреть файл

Before After
Width: 467  |  Height: 808  |  Size: 13KB

Двоичные данные
tee-scls2.png Просмотреть файл

Before After
Width: 1120  |  Height: 840  |  Size: 128KB

+ 423
- 0
wasora.tex Просмотреть файл

@@ -0,0 +1,423 @@
\lstdefinelanguage{wasora}{
morekeywords={
ABORT,
ADIABATIC,
ALGORITHM,
ALIAS,
AS,
ASCII_FILE,
ASCII_FILE_PATH,
BAKE,
BC,
BINARY_FILE,
BINARY_FILE_PATH,
BOUNDARY,
BREAK,
CALL,
CELLS,
CLOSE,
COLS,
COLUMNS,
CONST,
DATA,
DEFAULT_ARGUMENT_VALUE,
DEGREES,
DELTAEPSABS,
DELTAEPSREL,
DELTA_X,
DELTA_Y,
DELTA_Z,
DIFFERENTIAL,
DIMENSIONS,
DO_NOT_EVALUATE_AT_PARSE_TIME,
DO_NOT_OPEN,
DO_NOT_RERUN,
DO_NOT_SET_BLOCK_SIZE,
DUMP_FILE_PATH,
ELASTIC,
ELASTIC_AXISYMMETRIC,
ELEMS_PER_LINE,
ELSE,
ENDIF,
END_POINT,
EPSABS,
EPSREL,
EPS_TYPE,
EXPR,
EXPRESSION,
FILE,
FILE_PATH,
FINO_DEBUG,
FINO_LINEARIZE,
FINO_PROBLEM,
FINO_SOLVER,
FINO_STEP,
FIT,
FLUX_POST,
FORMAT,
FORMULATION,
FROM,
FUNCTION,
FUNCTION_DATA,
GAUSS_POINTS,
GRADIENT,
GRADIENT_EVALUATION,
GRADIENT_JACOBIAN_THRESHOLD,
GROUPS,
GUESS,
HEADER,
HEAT,
HEAT_AXISYMMETRIC,
HISTORY,
HORIZONTAL,
ID,
IF,
IGNORE_NULL,
I_MAX,
IMPLICIT,
IMPLICIT_BC,
INCLUDE,
INCLUDE_INPUT,
INCREMENTAL,
INDEX,
INITIAL_CONDITIONS_MODE,
INPUT,
INPUT_FILE,
INPUT_FILE_PATH,
INTERPOLATION,
INTERPOLATION_THRESHOLD,
IS,
JUST_BUILD,
JUST_SOLVE,
KSP_TYPE,
LENGTH_X,
LENGTH_Y,
LENGTH_Z,
LOAD_PLUGIN,
LOAD_ROUTINE,
M,
M4,
MACRO,
MATERIAL,
MATRICES_ASCII,
MATRICES_ASCII_STRUCTURE,
MATRICES_PETSC_ASCII,
MATRICES_PETSC_BINARY,
MATRICES_PETSC_COMPRESSED_BINARY,
MATRICES_PETSC_DENSE,
MATRICES_PETSC_OCTAVE,
MATRICES_SIZE,
MATRICES_SNG,
MATRICES_SNG_STRUCT,
MATRICES_STRIDE,
MATRICES_X,
MATRICES_X_SIZE,
MATRIX,
MAX,
MAX_DAUGHTERS,
MAX_ITER,
MB,
MEMORY_USAGE_SHMEM,
MESH,
MESH_FILL_VECTOR,
MESH_FIND_MAX,
MESH_INTEGRATE,
MESH_MAIN,
MESH_POST,
METHOD,
MILONGA_DEBUG,
MILONGA_PROBLEM,
MILONGA_SOLVER,
MILONGA_STEP,
MIN,
MINIMIZE,
MODAL,
MODE,
NAME,
NCELLS_X,
NCELLS_Y,
NCELLS_Z,
N_EIGEN,
NODES,
NOMESH,
NO_MESH,
NONEWLINE,
NO_PHYSICAL_NAMES,
NORERUN,
NOSEP,
NSTEPS,
OFFSET,
OFFSET_X,
OFFSET_Y,
OFFSET_Z,
OPEN,
OPTIMIZE,
ORDERING,
OUTER_STEPS,
OUTPUT,
OUTPUT_FILE,
OUTPUT_FILE_PATH,
OVER,
PARAMETRIC,
PC_TYPE,
PEAK,
PHASE_SPACE,
PHYSICAL_ENTITY,
PHYSICAL_PROPERTY,
PLANE_STRAIN,
PLANE_STRESS,
PRINT,
PRINT_FUNCTION,
PRINT_VECTOR,
PROGRESS_ASCII,
PROGRESS_BUILD_SHMEM,
PROGRESS_SOLVE_SHMEM,
RANGE_MAX,
RANGE_MIN,
READ,
READ_DATA,
READ_FUNCTION,
RERUN,
RESIDUALS,
RESULT,
ROUTINE,
ROWS,
SCALE_FACTOR,
SCHEME,
SEM,
SEMAPHORE,
SEP,
SEPARATOR,
SET_BLOCK_SIZE,
SET_NEAR_NULLSPACE,
SET_NEAR_NULL_SPACE,
SHAKE,
SHELL,
SHEPARD_EXPONENT,
SHEPARD_RADIUS,
SHM,
SHMEM_MEMORY,
SHMEM_PROGRESS_BUILD,
SHMEM_PROGRESS_SOLVE,
SHM_OBJECT,
SIMAN_EFUNC,
SIZE,
SIZES,
SOLUTION,
SOLUTION_NAMES,
SOLUTIONS,
SOLVE,
SPECTRUM,
ST_ANTI_SHIFT,
START_POINT,
STEP,
STRING,
STRUCTURED,
ST_SHIFT,
ST_TYPE,
SUBSPACE_DIM,
SYMMETRY_AXIS,
TEXT,
TIME_PATH,
TO,
TOTAL,
TYPE,
UNKNOWN,
UNKNOWNS,
VAR,
VECTOR,
VECTOR_DATA,
VECTORS,
VERBOSE,
VERTICAL,
VIA,
VOLHOM,
WRITE,
X_INCREASES_FIRST,
X_MAX,
XS,
Y_MAX,
Z_MAX,
ALLOWED,
AS_PROVIDED,
FROM_DERIVATIVES,
FROM_VARIABLES,
GRADTOL,
MAX_ITER,
NONE,
POST,
SKIP_HEADER_STEP,
SKIP_STATIC_STEP,
SKIP_STEP,
SKIP_TIME,
TOL,
WAIT,
},
morekeywords={[2]
},
morekeywords={[3]
cells,
cells_0,
done,
done_0,
done_outer,
done_outer_0,
done_static,
done_static_0,
done_transient,
done_transient_0,
dont_quit,
dont_quit_0,
dont_report,
dont_report_0,
dt,
dt_0,
elements,
elements_0,
end_time,
end_time_0,
eps,
eps_0,
i,
i_0,
infinite,
infinite_0,
in_outer_initial,
in_outer_initial_0,
in_static,
in_static_0,
in_static_first,
in_static_first_0,
in_static_last,
in_static_last_0,
in_transient,
in_transient_0,
in_transient_first,
in_transient_first_0,
in_transient_last,
in_transient_last_0,
j,
j_0,
max_dt,
max_dt_0,
min_dt,
min_dt_0,
ncores,
ncores_0,
nodes,
nodes_0,
on_gsl_error,
on_gsl_error_0,
on_ida_error,
on_ida_error_0,
on_nan,
on_nan_0,
pi,
pi_0,
pid,
pid_0,
quit,
quit_0,
realtime_scale,
realtime_scale_0,
rel_error,
rel_error_0,
report,
report_0,
static_steps,
static_steps_0,
step_inner,
step_inner_0,
step_outer,
step_outer_0,
step_static,
step_static_0,
step_transient,
step_transient_0,
t,
t_0,
x,
x_0,
y,
y_0,
z,
z_0,
zero,
zero_0,
},
morekeywords={[4]
abs,
acos,
asin,
atan,
atan2,
builtindecl.h,
ceil,
clock,
cos,
cosh,
d_dt,
deadband,
derivative,
equal,
exp,
expint1,
expint2,
expint3,
expintn,
floor,
func_min,
gauss_kronrod,
gauss_legendre,
heaviside,
if,
integral,
integral_dt,
integral_euler_dt,
is_even,
is_in_interval,
is_odd,
j0,
lag,
lag_bilinear,
lag_euler,
last,
limit,
limit_dt,
log,
mark_max,
mark_min,
max,
min,
mod,
not,
prod,
random,
random_gauss,
root,
round,
sawtooth_wave,
sgn,
sin,
sinh,
sqrt,
square_wave,
sum,
tan,
tanh,
threshold_max,
threshold_min,
triangular_wave,
vecdot,
vecmax,
vecmaxindex,
vecmin,
vecminindex,
vecnorm,
vecsize,
vecsum,
},
sensitive=true,
morecomment=[l]{\#},
morestring=[b]\",
}

Редактирование Предпросмотр
Загрузка…
Отмена
Сохранить