cufens

meta.yaml

@@ -12,7 +12,7 @@ colorlinks: true
 linkReferences: true
 nameInLink: true
 mathspec: true
-formats: html tex pdf
+formats: html tex pdf epub
 listings: true
 template: simple
 ...

nafems4.md

@@ -1102,22 +1102,28 @@ Back and distantly, in\ [@sec:case] we said that people noticed there were some
 
 ## In air (ASME’s basic approach) {#sec:in-air}
 
-We already said in\ [@sec:fatigue] that fatigue analysis gives the limit number\ $N$ of cycles that a certain mechanical part can withstand when subject to a certain periodic load of stress amplitude\ $S_\text{alt}$. If the actual number of cycles\ $n$ the load is applied is smaller than the limit\ $N$, then the part is fatigue-resistant. In our case study there is a mixture of several periodic loads, each one expected to occur a certain number of times. ASME’s way to evaluate the resistance is to break up the stress history into partial stress amplitudes\ $S_{\text{alt},j}$ and compute individual usage factors\ $U_k$ for the\ $k$-th amplitude as
+We already said in\ [@sec:fatigue] that fatigue analysis gives the limit number\ $N$ of cycles that a certain mechanical part can withstand when subject to a certain periodic load of stress amplitude\ $S_\text{alt}$. If the actual number of cycles\ $n$ the load is applied is smaller than the limit\ $N$, then the part is fatigue-resistant. In our case study there is a mixture of several periodic loads, each one expected to occur a certain number of times. ASME’s way to evaluate the resistance is to break up the stress history into partial stress amplitudes\ $S_{\text{alt},j}$ between a “peak” and a “valley” and compute individual usage factors\ $U_j$ for the\ $j$-th amplitude (which does not need to coincide with a full cycle\ $k$) as
 
-$$U_k = \frac{n_k}{N_k}$$
+$$U_j = \frac{n_j}{N_j}$$
+
+The overall cumulative usage factor is then the algebraic sum of the partial contributions
+
+$$\text{CUF} = U_1 + U_2 + \dots + U_j + \dots$$
+
+If\ $\text{CUF} < 1$, then the part under analysis can withstand the proposed cyclic operation.
 
 If the extrema of the partial stress amplitude correspond to different transients, then the following note in ASME-3224(5) should be followed:
 
-> In determining $n_1$, $n_2$, $n_3$, $\dots$, $n_k$ consideration shall be given to the superposition of cycles of various origins which produce a total stress difference range greater than the stress difference ranges of the individual cycles. For example, if one type of stress cycle produces 1,000 cycles of a stress difference variation from zero to +60,000\ psi and another type of stress cycle produces 10,000 cycles of a stress difference variation from zero to −50,000\ psi, the two types of cycle to be considered are defined by the following parameters:
+> In determining $n_1$, $n_2$, $n_3$, $\dots$, $n_j$ consideration shall be given to the superposition of cycles of various origins which produce a total stress difference range greater than the stress difference ranges of the individual cycles. For example, if one type of stress cycle produces 1,000 cycles of a stress difference variation from zero to +60,000\ psi and another type of stress cycle produces 10,000 cycles of a stress difference variation from zero to −50,000\ psi, the two types of cycle to be considered are defined by the following parameters:
 >
 > (a) for type 1 cycle, $n_1 =$ 1,000 and $S_{\text{alt},1} = (60,000 + 50,000)/2 = 55,000$\ psi;
 > (b) for type 2 cycle, $n_2 =$ 9,000 and $S_{\text{alt},2} = (50,000 + 0)/2 = 25,000$\ psi.
 
-This cryptic paragraph can be better explained by using a clearer example. To avoid using actual sensitive data from a real power plant, let us use the same test case used by both the NRC (in its report NUREG/CR-6909) and EPRI (report 1025823) called “EAF SAmple PRoblem 2-Rev. \2 (10/21/2011)”.
+This cryptic paragraph can be better explained by using a clearer example. To avoid using actual sensitive data from a real power plant, let us use the same test case used by both the NRC (in its report NUREG/CR-6909) and EPRI (report 1025823) called “EAF (Environmentally-Assisted Fatigue) Sample Problem 2-Rev.\ 2 (10/21/2011)”.
 
 ![A low-alloy steel vessel nozzle (blue) welded to a stainless steel pipe (gray).](axi-inches-3d.png){#fig:axi-inches-3d width=60%}
 
-It consists of a typical vessel (NB-3200) nozzle with attached piping (NB-3600) as illustrated in\ [@fig:axi-inches-3d]. These components are subject to four transients, that give rise to linearized stress histories (slightly modified according to NB-3216.2) which are given as individual stress values juxtaposed so as to span a time range of about 36,000 seconds ([@fig:nureg1]). As the time steps is not constant, each stress value has an integer index\ $i$ that uniquely identifies it:
+It consists of a typical vessel (NB-3200) nozzle with attached piping (NB-3600) as illustrated in\ [@fig:axi-inches-3d]. These components are subject to four transients\ $k=1,2,3,4$ that give rise to linearized stress histories (slightly modified according to NB-3216.2) which are given as individual stress values juxtaposed so as to span a time range of about 36,000 seconds ([@fig:nureg1]). As the time steps is not constant, each stress value has an integer index\ $i$ that uniquely identifies it:
 
 | Transient number\ $k$ | Time range [s] | Index range | Number of cycles\ $n_k$ |
 |:---------------------:|:--------------:|:-----------:|:-----------------------:|
@@ -1135,7 +1141,7 @@ A design-basis earthquake was assumed to occur briefly during one second at arou
 
 ![Detail of the earthquake](nureg3.svg){#fig:nureg3 width=80%}
 
-Linearised stress\ $\text{MB}_{31}$ time history of the example problem from NRC and EPRI. The id of the extrema are shown in green (minimums) and red (maximums).
+Linearised stress\ $\text{MB}_{31}$ time history of the example problem from NRC and EPRI. The indexes\ $i$ of the extrema are shown in green (minimums) and red (maximums).
 :::::
 
 To compute the global usage factor, we first need to find all the combinations of local extrema pairs and then sort them in decreasing order of stress difference. For example, the largest stress amplitude is found between $i=447$ and $i=694$. The second one is 447-699. Then 699-1020, 699-899, etc. For each of these pairs, defined by the indexes\ $i_{1,j}$ and $i_{2,j}$, a partial usage factor\ $U_j$ should computed. The stress amplitude\ $S_{\text{alt},j}$ which should be used to enter into the $S$-$N$ curve is
@@ -1143,7 +1149,7 @@ To compute the global usage factor, we first need to find all the combinations o
 $$
 S_{\text{alt},j} = \frac{1}{2} \cdot k_{e,j} \cdot \left| MB^\prime_{i_{1,j}} - MB^\prime_{i_{2,j}} \right| \cdot \frac{E_\text{SN}}{E(T_{\text{max}_j})}
 $$
-where $k_e$ is a plastic correction factor for large loads (NB-3228.5), $E_\text{SN}$ is the Young Modulus used to creat the $S$-$N$ curve (provided in the ASME fatigue curves) and\ $E(T_{\text{max}_j})$ is the material’s Young Modulus at the maximum temperature within the interval.
+where $k_e$ is a plastic correction factor for large loads (NB-3228.5), $E_\text{SN}$ is the Young Modulus used to creat the $S$-$N$ curve (provided in the ASME fatigue curves) and\ $E(T_{\text{max}_j})$ is the material’s Young Modulus at the maximum temperature within the\ $j$-th interval.
 
 We now need to comply with ASME’s obscure note about the number of cycles to assign a proper value of\ $n_j$. Back to the largest pair 447-694, we see that 447 belongs to transient\ #1 which has $n_1=20$ and 694 belongs to the earthquake with\ $n_e=5$. Therefore\ $n_1=5$, and the cycles associated to each index are decreased in five. So $i=694$ disappears and the number of cycles associated to $i=447$ are decreased from 20 to 15. The second largest pair is now 447-699, with 15 (because we just spent 5 in the first pair) and 50 cycles respectively. Now $n_2=15$, point\ 447 disappears and 699 remains with 35 cycles. The next pair is 699-1020, with number of cycles 35 and 20 so $n_3=20$, point 1020 disappears and 699 remains with 15 cycles. And so on, down to the last pair.
 
@@ -1152,40 +1158,64 @@ We now need to comply with ASME’s obscure note about the number of cycles to a
 
 ![Results reproduced by the author](cuf-seamplex.png){#fig:cuf-seamplex width=100%}
 
-Tables of individual usage factors for the NRC/EPRI example. One table is taken from a document issued by almost-a-billion-dollar-year-budget government agency from the most powerful country in the world and the other one is from a third-world engineering startup.
+Tables of individual usage factors for the NRC/EPRI “EAF Sample Problem 2-Rev.\ 2 (10/21/2011).” One table is taken from a document issued by almost-a-billion-dollar-year-budget government agency from the most powerful country in the world and the other one is from a third-world engineering startup.
 :::::
 
-Why all these details? Not because I want to teach you how to perform fatigue evaluations just reading this section without resorting to ASME, fatigue books and even other colleagues. It is to show that even though these computation can be made “by hand” (i.e. using a calculator or, God forbids, a spreadsheet) when having to evaluate a few SCLs within several piping systems it is far (and I mean really far) better to automatise all these steps by writing a set of scripts. Not only will the time needed to process the information be reduced, but also the
-introduction of human errors be minimised and repeatability of results will be assured. This is true in general, so here is another tip: learn to write scripts to post-process your FEM results (you will need to use a script-friendly FEM program) and you will gain considerable margins regarding time and quality.
+Why all these details? Not because I want to teach you how to perform fatigue evaluations just reading this section without resorting to ASME, fatigue books and even other colleagues. It is to show that even though these computation can be made “by hand” (i.e. using a calculator or, God forbids, a spreadsheet) when having to evaluate a few SCLs within several piping systems it is far (and I mean really far) better to automatise all these steps by writing a set of scripts. Not only will the time needed to process the information be reduced, but also the introduction of human errors will be minimised and repeatability of results will be assured. This is true in general, so here is another tip: learn to write scripts to post-process your FEM results (you will need to use a script-friendly FEM program) and you will gain considerable margins regarding time and quality.
 
 ## In water (NRC’s extension)
 
-cufen, la idea es la misma hacer con scripts, ponerse de acuerdo con el cliente, cianto queres que de, el weoghting de stevens no esta claro creo que porque no quisieron poner ecuaciones complicadas, y eso es peor porque las palabras son ambiguas
+The fatigue curves and ASME’s (both\ III and VIII) methodology to analyse cyclic operations assume the parts under study are in contact with air, which is not the case of nuclear reactor pipes. Insteado of building a brand new body of knowledge to replace ASME, the NRC decided to modify the former adding environmentally-assisted fatigue multipliers to the traditional usage factors, defined as
 
-Environmentally assisted fatigue
+$$F_\text{en} = \frac{N_\text{air}}{N_\text{water}} \geq 1$$
 
-1025823
+This way, the environmentally-assisted usage factor for the $k$-th load pair is
 
+$$\text{CUF}_\text{en,j} = U_j \cdot {F_\text{en},j}$$
+and the global cumulative usage factor in water is the sum of these partial contributions
 
-fatigue mutiplier
+$$\text{CUF}_\text{en} = U_1 \cdot F_{\text{en},1} + U_2 \cdot F_{\text{en},2} + \dots + U_j \cdot F_{\text{en},j} + \dots$${#eq:cufen}
 
-$$F_\text{en} = \frac{N_\text{air}}{N_\text{water}}$$
+In EPRI words:
 
-EPRI:
-
-The general steps for performing an EAF analysis are as follows:
-(1) perform an ASME fatigue analysis using fatigue curves for an air
+> The general steps for performing an EAF analysis are as follows:
+>
+>  1. perform an ASME fatigue analysis using fatigue curves for an air
 environment
-(2) calculate Fen factors for each transient pair in the fatigue analysis
-(3) apply the Fen factors to the incremental usage calculated for each
-transient pair (Ui), to determine the CUFen, using Equation 3-1.
+>  2. calculate $F_\text{en}$ factors for each transient pair in the fatigue analysis
+>  3. apply the $F_\text{en}$ factors to the incremental usage calculated for each
+transient pair ($U_j$), to determine the $\text{CUF}_\text{en}$, using\ [@eq:cufen]
+
+Again, if $\text{CUF}_\text{en} < 1$, then the system under study can withstand the assumed cyclic loads. Note that as\ $F_{\text{en},j}$, we can have $\text{CUF} < 1$ and $\text{CUF}_\text{en} > 1$ at the same time.
+
+
+The NRC has performed a comprehensive set of theoretical and experimental tests to study and analyse the nature and dependence of the non-dimensional correction factors\ $F_\text{en}$. They found that, for a given material, they depend on:
+
+ a. the concentration\ $O(t)$ of dissolved oxygen in the water,
+ b. the temperature\ $T(t)$ of the pipe,
+ c. the strain rate\ $\dot{\epsilon}(t)$, and
+ d. the content of sulfur\ $S(t)$ in the pipes (only for carbon or low-allow steels).
 
+Apparently it makes no difference whether the environment if composed of either light or heavy water. There are somewhat different sets of non-dimensional analytical expressions that give the value of\ $F_{\text{en}}(t)$, both in the few revisions of NUREG/6909 and in EPRI’s report \#1025823. Although they are not important now, the actual expressions should be defined and agreed with the plant owner and the regulator. The main result is that\ $F_{\text{en}}(t)=1$ if\ $\dot{\epsilon}(t)\leq0$, i.e. there are no environmental effects during the time intervals where the pipe is being compressed.
+
+Once we have the instantaneous factor\ $F_{\text{en}}(t)$, we need to obtain an average value\ $F_{\text{en},j}$ which should be applied to the\ $j$-th load pair. Again, there are a few different ways of lumping the time-dependent\ $F_{\text{en}}(t)$ into a single $F_{\text{en},j}$ for each interval. Both NRC and EPRI give simple equations that depend on particular time discretization of the stress histories that, in my view, are all ill-defined. My guess is that they underestimated they audience and feared readers would not understand the slightly-more complex mathematics needed to correctly define the problem. The result is that they introduced a lot of ambiguities (and even technical errors) just not to offend the maths illiterate. A decision I do not share, and a another reason to keep on learning and practising math.
+
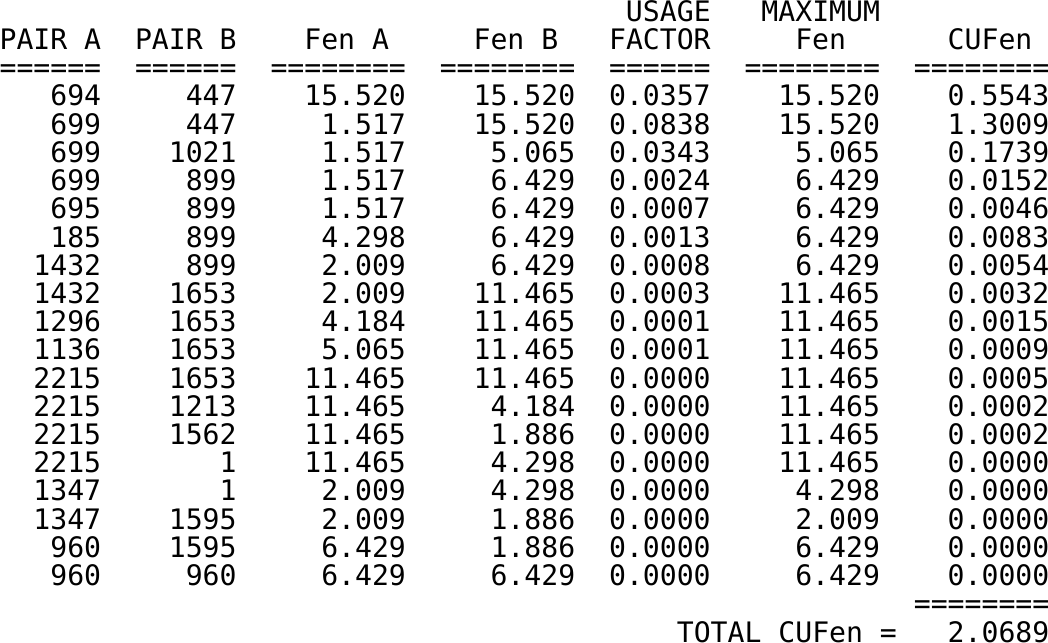
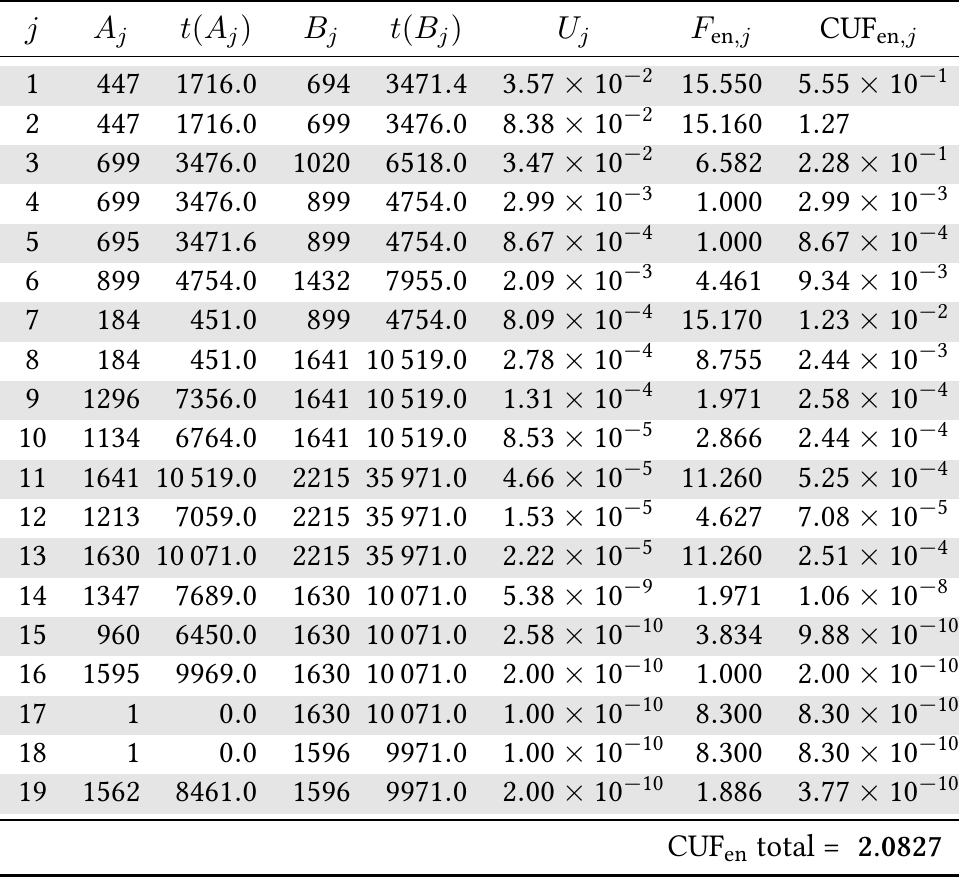
+Back in the case study, I have come up with a weighting method that I claim is less ill-defined (it still is for border-line cases) and which the plain owner accepted as valid. [@Fig:cufen] shows the reference results of the problem and the ones obtained with the proposed method (based on computing two correction factors and then taking the maximum). Note how in\ [@fig:cufen-nrc], pairs 694-447 and 699-447 have the same\ $F_\text{en}$ even though they are (marginally) different. The results from\ [@fig:cufen-seamplex] give two (marginally) different correction factors.
+
+::::: {#fig:cufen}
+![Results according to the author of NUREG/6909 corresponding to the latest draft of the document.](cufen-nrc.png){#fig:cufen-nrc width=100%}
+
+![Results reproduced by the author using his own weighting scheme.](cufen-seamplex.png){#fig:cufen-seamplex width=100%}
+
+Tables of individual environmental correction and usage factors for the NRC/EPRI “EAF Sample Problem 2-Rev.\ 2 (10/21/2011).” The reference method assigns the same\ $F_\text{en}$ to the first two rows whilst the proposed lumping scheme does show a difference.
+:::::
 
 
-$$\text{CUF}_\text{en} = U_1 \cdot F_{\text{en},1} + U_2 \cdot F_{\text{en},2} + \dots + U_n \cdot F_{\text{en},n}$$
 
 # Errors and uncertainties
 
+los cufens son parecidos
+
 errors and uncertainties: model parameters (is E what we think? is the material linear?), geometry (does the CAD represent the reality?) equations (any effect we did not have take account), discretization (how well does the mesh describe the geometry?)
 
 do you trust your FEM program?
@@ -1222,7 +1252,7 @@ experimento de millikan
  * the elastic problem is still linear after all
  * keep in mind that FEM are a mean to get an engineering solution, not and end by themselves
  * learn to write scripts to post-process FEM results (from a script-friendly FEM program)
-
+ * clone the [environmental fatigue sample problem repository](https://bitbucket.org/seamplex/) and run the scripts to solve the NRC/EPRI  [@sec:parametric] were built and expand them to cover “we might go on...” bullets
 
 # Referenced works