14 changed files with 7257 additions and 21 deletions
+ 1961
- 0
dominio-continuo.svg
File diff suppressed because it is too large
View File
+ 3197
- 0
dominio-estructurado.svg
File diff suppressed because it is too large
View File
+ 2000
- 0
dominio-no-estructurado.svg
File diff suppressed because it is too large
View File
+ 1
- 1
meta.yaml
View File
| @@ -1,6 +1,6 @@ | |||
| --- | |||
| title: Fatigue Analysis in Nuclear Piping | |||
| subtitle: A journey from college theory to an actual engineering problem | |||
| subtitle: A journey from college theory to solving an actual engineering problem | |||
| author: Jeremy Theler | |||
| authoremail: jeremy@seamplex.com | |||
| fontsize: 11pt | |||
+ 98
- 20
nafems4.md
View File
| @@ -2,7 +2,7 @@ | |||
| First of all, please take this text as a written chat between you an me, i.e. an average engineer that have already taken the journey from college to performing actual engineering using finite element analysis and has something to say about it. Picture yourself in a coffee bar, talking and discussing concepts and ideas with me. Maybe needing to go to a blackboard (or notepad?). Even using a tablet to illustrate some three-dimensional results. But always as a chat between colleagues. | |||
| Please also note that I am not a mechanical engineer, although I shared many undergraduate courses with some of them. I am a nuclear engineer with a strong background on mathematics and computer programming. I went to college between 2002 and 2008. Probably a lot of things have changed since then---at least that is what these millenials guys and girls seem to be boasting about---but chances are we all studied solid mechanics and heat transfer with a teacher using a piece of chalk on a blackboard and students writing down notes with pencils on paper sheets. And there is really not much that one can do with pencil and paper regarding mechanical analysis. Any actual case worth the time of an engineer need to be more complex than an ideal canonical case with analytical solution. | |||
| Please also note that I am not a mechanical engineer, although I shared many undergraduate courses with some of them. I am a nuclear engineer with a strong background on mathematics and computer programming. I went to college between 2002 and 2008. Probably a lot of things have changed since then---at least that is what these “millenials” guys and girls seem to be boasting about---but chances are we all studied solid mechanics and heat transfer with a teacher using a piece of chalk on a blackboard and students writing down notes with pencils on paper sheets. And there is really not much that one can do with pencil and paper regarding mechanical analysis. Any actual case worth the time of an engineer need to be more complex than an ideal canonical case with analytical solution. | |||
| We will be swinging back and forth between a case study about fatigue analysis in piping systems of a nuclear power plant and more generic and even romantic topics related to finite elements and computational mechanics. These latter regressions will not remain just as abstract theoretical ideas. Not only will they be directly applicable to the development of the main case, but they will also apply to a great deal of other engineering problems tackled with the finite element method. | |||
| @@ -28,11 +28,11 @@ Another heads up is that we will dig into some math. Probably it would be be sim | |||
| Piping systems in sensitive industries like nuclear or oil & gas should be designed and analysed following the recommendations of an appropriate set of codes and norms, such as the ASME\ Boiler and Pressure Vessel Code. | |||
| This code of practice (book) was born during the late\ XIX century, before finite-element methods for solving partial differential equations were even developed. And much longer before they were available for the general engineering community. Therefore, much of the code assumes design and verification is not necessarily performed numerically but with paper and pencil (yes, like in college). However, it still provides genuine guidance in order to ensure pressurised systems behave safely and properly without needing to resort to computational tools. Combining finite-element analysis with the ASME code gives the cognisant engineer a unique combination of tools to tackle the problem of designing and/or verifying pressurised piping systems. | |||
| In the years following Enrico Fermi’s demonstration that a self-sustainable fission reaction chain was possible (actually, in fact after WWII was over), people started to build plants in order to transform the energy stored within the atoms nuclei into usable electrical power. They quickly reached the conclusion that high-pressure heat exchangers and turbines were needed. So they started to follow the ASME\ Boiler and Pressure Vessel Code. They also realised that some requirements did not fit the needs of the nuclear industry. But instead of writing a new code from scratch, they added a new chapter to the existing body of knowledge: the celebrated ASME Section\ III. | |||
| In the years following [Enrico Fermi](https://en.wikipedia.org/wiki/Enrico_Fermi)’s demonstration that a self-sustainable fission reaction chain was possible (actually, in fact, after WWII was over), people started to build plants in order to transform the energy stored within the atoms nuclei into usable electrical power. They quickly reached the conclusion that high-pressure heat exchangers and turbines were needed. So they started to follow the ASME\ Boiler and Pressure Vessel Code. They also realised that some requirements did not fit the needs of the nuclear industry. But instead of writing a new code from scratch, they added a new chapter to the existing body of knowledge: the celebrated ASME Section\ III. | |||
| After further years passed by, engineers (probably the same people that forked section\ III) noticed that fatigue in nuclear power plants was not exactly the same as in other piping systems. There were some environmental factors directly associated to the power plant that was not taken into account by the regular ASME code. Again, instead of writing a new code from scratch, people decided to add correction factors to the previously amended body of knowledge. This is how knowledge evolves, and it is this kind of complexities that engineers are faced with during their professional lives. We have to face it, it would be a very hard work to re-write everything from scratch every time something changes. | |||
|  | |||
| {#fig:real-life} | |||
| Actually, this article does not focus on a single case study but on some general ideas regarding analysis of fatigue in piping systems in nuclear power plants. There is no single case study but a compendium of ideas obtained by studying many different systems which are directly related to the safety of a real nuclear reactor. | |||
| @@ -103,7 +103,7 @@ What does this all have to do with mechanical engineering? Well, once we know wh | |||
| ## An infinitely-long pressurised pipe | |||
| Let us proceed to a our second step, and consider an infinite pipe subject to uniform internal pressure. Actually, we are going to solve the mechanical problem on an infinite hollow cylinder, which looks like pipe. This case is usually tackled in college courses, and chances are you already solved it. Actually, the first (and simpler) problem is the “thin cylinder problem.” Then, the “thick cylinder problem” is introduced, which is slightly more complex. Nevertheless, it has an analytical solution which is derived in [@pipe-linearized]. For the present case, Let us consider an infinite pipe (i.e. a hollow cylinder) of internal radius $a$ and external radius $b$ with uniform mechanical properties---Young modulus $E$ and Poisson’s ratio $\nu$---subject to an internal uniform pressure $p$. | |||
| Let us proceed to a our second step, and consider an infinite pipe subject to uniform internal pressure. Actually, we are going to solve the mechanical problem on an infinite hollow cylinder, which looks like pipe. This case is usually tackled in college courses, and chances are you already solved it. Actually, the first (and simpler) problem is the “thin cylinder problem.” Then, the “thick cylinder problem” is introduced, which is slightly more complex. Nevertheless, it has an analytical solution which is derived [here](https://www.seamplex.com/fino/doc/pipe-linearized/). For the present case, Let us consider an infinite pipe (i.e. a hollow cylinder) of internal radius $a$ and external radius $b$ with uniform mechanical properties---Young modulus $E$ and Poisson’s ratio $\nu$---subject to an internal uniform pressure $p$. | |||
| ### Displacements | |||
| @@ -180,7 +180,15 @@ Each of these methods (also called schemes) have of course their own features, p | |||
| a. structured, or | |||
| b. unstructured | |||
| [Figure@fig:grids] illustrate how the same domain can be discretized using these two kind of grids. In the first case, we could identify any single cell by using just two indexes. We could even tell which nodes define each cell just from these indexes. In the second case, we need an explicit list first to know how many cells there are. Even more, there is no way to link the nodes with the cells (back and forth) other than having a list of nodes and cells. Again, there are pros and cons for each of the grid types such as simplicity, flexibility, etc. In general, unstructured grids and better represent a certain geometry with the same number of cells. Structured grids suffer the so-called “staircase effect” that makes the unusable for discretizing mechanical parts. | |||
| Figure [-@fig:grids] illustrates how the same domain can be discretized using these two kind of grids. In the first case, we could identify any single cell by using just two indexes. We could even tell which nodes define each cell just from these indexes. In the second case, we need an explicit list first to know how many cells there are. Even more, there is no way to link the nodes with the cells (back and forth) other than having a list of nodes and cells. Again, there are pros and cons for each of the grid types such as simplicity, flexibility, etc. In general, unstructured grids and better represent a certain geometry with the same number of cells. Structured grids suffer the so-called “staircase effect” that makes the unusable for discretizing mechanical parts. | |||
| ::::: {#fig:grids} | |||
| {#fig:continuous width=30%} | |||
| {#fig:structured width=30%} | |||
| {#fig:unstructured width=30%} | |||
| Discretization of a spatial domain | |||
| ::::: | |||
| The first of the three methods is based on approximating derivative (i.e. differentials) by incremental quotients (i.e. differences). The second one heavily relies on geometrical ideas rather than on pure mathematical grounds. Finally, our beloved finite elements are the most “mathematical” ones. Actually, a complete derivation of the finite element method can be written in a textbook without requiring a single figure, just like D’Alembert did more than two centuries ago. In any case, it is important to note that finite differences and elements compute results at the _nodes_ of a mesh, whilst finite volumes compute results at the _cells_ of a mesh. Finally, any method may be used in structured grids but only finite elements and volumes are especially suited for working with unstructured grids. | |||
| @@ -189,7 +197,7 @@ There are technical reasons that justify why the finite element method is the ki | |||
| Before proceeding, I would like to make two comments about common nomenclature. The first one is that if we exchanged the words “volumes” and “elements” in all the written books and articles, nobody would note the difference. There is nothing particular in both theories that can justify why finite volumes use volumes and finite elements use elements. Actually volumes and elements are the same geometric constructions. The names were randomly assigned. | |||
| The second one is more philosophical and refers to the word “simulation” which is often used to refer to solving a problem using a numerical scheme such as the finite element method. [I am against at using this word for this endeavour](https://www.seamplex.com/blog/say-modeling-not-simulation.html). The term simulation has a connotation of both “pretending” and “faking” something, that is definitely not what we are doing when solving an engineering problem with finite elements. Sure there are some cases in which we simulate, such as using the Monte Carlo method (originally used by Fermi as an attempt to understand how neutrons behave in the core of nuclear reactors). But when solving deterministic mechanical engineering problems I would rather say “modelling” than “simulation.” | |||
| The second one is more philosophical and refers to the word “simulation” which is often used to refer to solving a problem using a numerical scheme such as the finite element method. [I am against at using this word to refer to this endeavour](https://www.seamplex.com/blog/say-modeling-not-simulation.html). The term simulation has a connotation of both “pretending” and “faking” something, that is definitely not what we are doing when solving an engineering problem with finite elements. Sure there are some cases in which we simulate, such as using the Monte Carlo method (originally used by Fermi as an attempt to understand how neutrons behave in the core of nuclear reactors). But when solving deterministic mechanical engineering problems I would rather say “modelling” than “simulation.” | |||
| ## Kinds of finite elements {#sec:kinds} | |||
| @@ -233,7 +241,7 @@ Finally, when then uncertainties associated to the parameters, methods and model | |||
| 2. performing a large number of runs for different combination of parameters, and | |||
| 3. combining all the results into to obtain a best-estimate value plus uncertainty. | |||
| This kind of computation is usually required by the nuclear regulatory authorities when power plant designers need to address the safety of the reactors. What is the heat capacity of uranium above 1000ºC? What is the heat transfer coefficient when approaching the [critical heat flux](https://en.wikipedia.org/wiki/Critical_heat_flux) before the [Leidenfrost effect](https://en.wikipedia.org/wiki/Leidenfrost_effect)? A certain statistical analysis has to be done prior to actually parametrically swifting the input parameters so as to obtain a distribution of possible outcomes. | |||
| This kind of computation is usually required by the nuclear regulatory authorities when power plant designers need to address the safety of the reactors. What is the heat capacity of uranium above 1000ºC? What is the heat transfer coefficient when approaching the [critical heat flux](https://en.wikipedia.org/wiki/Critical_heat_flux) before the [Leidenfrost effect](https://en.wikipedia.org/wiki/Leidenfrost_effect) occurs? A certain statistical analysis has to be done prior to actually parametrically swifting the input parameters so as to obtain a distribution of possible outcomes. | |||
| **------** | |||
| @@ -313,7 +321,7 @@ divert(0) | |||
| So we need to address the issue of fatigue in nuclear reactor pipes that | |||
| 1. have cross-section changes, branches, valves, etc. | |||
| 1. are not infinite and have cross-section changes, branches, valves, etc. | |||
| 2. are made of different materials, | |||
| 3. are fixed at different locations to the wall through piping supports, | |||
| 4. are subject to | |||
| @@ -321,7 +329,7 @@ So we need to address the issue of fatigue in nuclear reactor pipes that | |||
| b. heat transients, and | |||
| c. seismic loads. | |||
| As I wanted to illustrate in [@sec:five], it is very important to decide what kind of problem (actually problems) we should be dealing with. As a nuclear engineer, I learned (after college) that there are some models that let you see some effects and some that let you see other effects.^[Please [say “modeling” not “simulation.”](https://www.seamplex.com/blog/say-modeling-not-simulation.html)] And even if it is in principle true that more complex models should let you see more stuff, they practically might show you nothing at all if the model is so big and complex that cannot fit into a computer (say because it needs hundreds of gigabytes of RAM to run) or because it takes more time to compute than you may have to deliver a report. | |||
| As I wanted to illustrate in [@sec:five], it is very important to decide what kind of problem (actually problems) we should be dealing with. As a nuclear engineer, I learned (theoretically in college but practically after college) that there are some models that let you see some effects and some that let you see other effects.^[Please [say “modeling” not “simulation.”](https://www.seamplex.com/blog/say-modeling-not-simulation.html)] And even if it is in principle true that more complex models should let you see more stuff, they definitely might show you nothing at all if the model is so big and complex that it doe not fit into a computer (say because it needs hundreds of gigabytes of RAM to run) or because it takes more time to compute than you may have before the final report is expected. | |||
| First of all, we should note that we need to solve | |||
| @@ -335,18 +343,89 @@ So for each time of the transient, the pipes are subject to | |||
| b. a uniform internal temperature $T_i(t)$ that gives rise to a non-trivial time-dependent temperature distribution\ $T(\vec{x},t)$ in the bulk of the pipes, and | |||
| c. internal distributed forces\ $\vec{f}=\rho \cdot \vec{a}$ at those times where the design earthquake is assumed to act. | |||
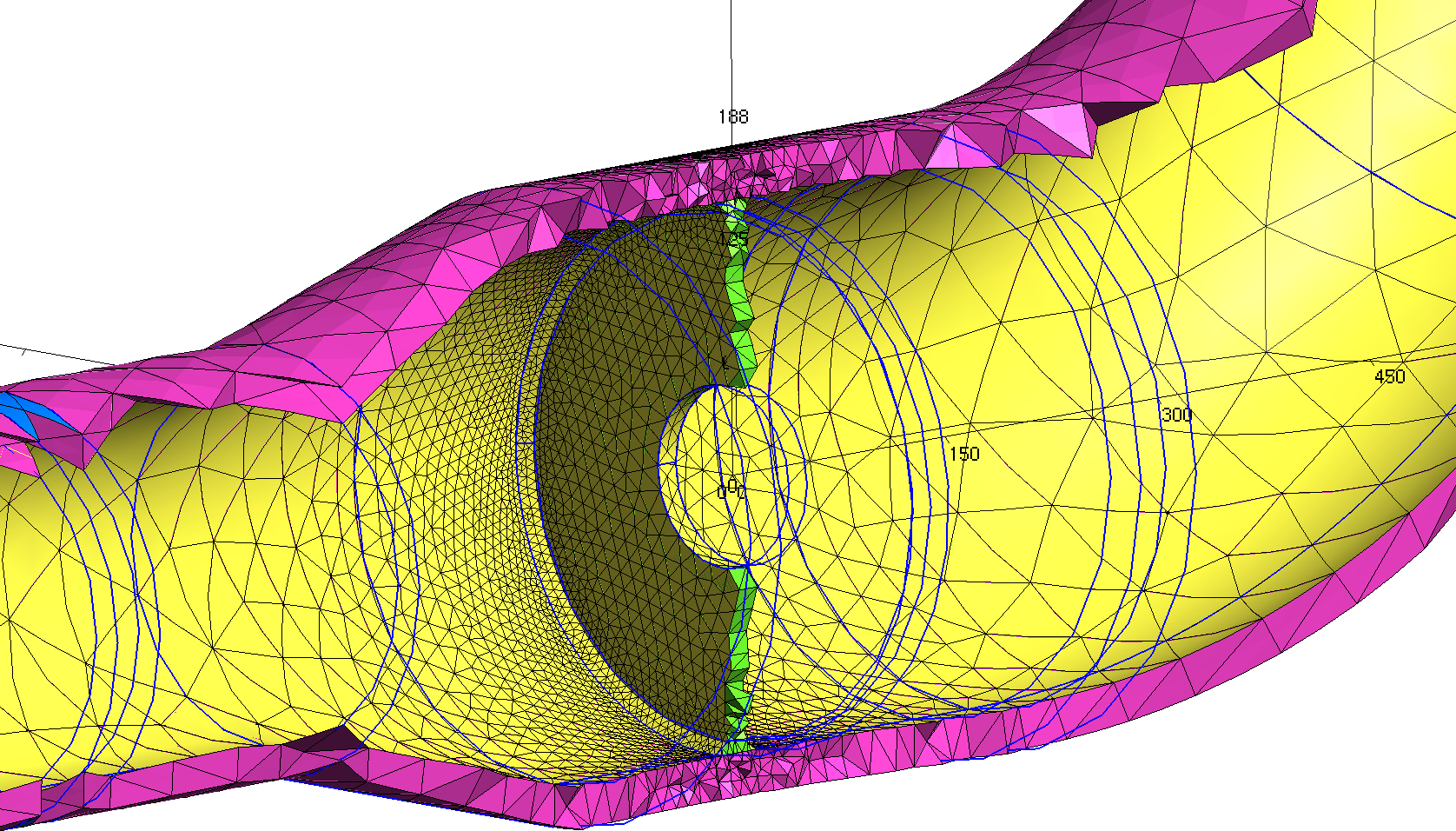
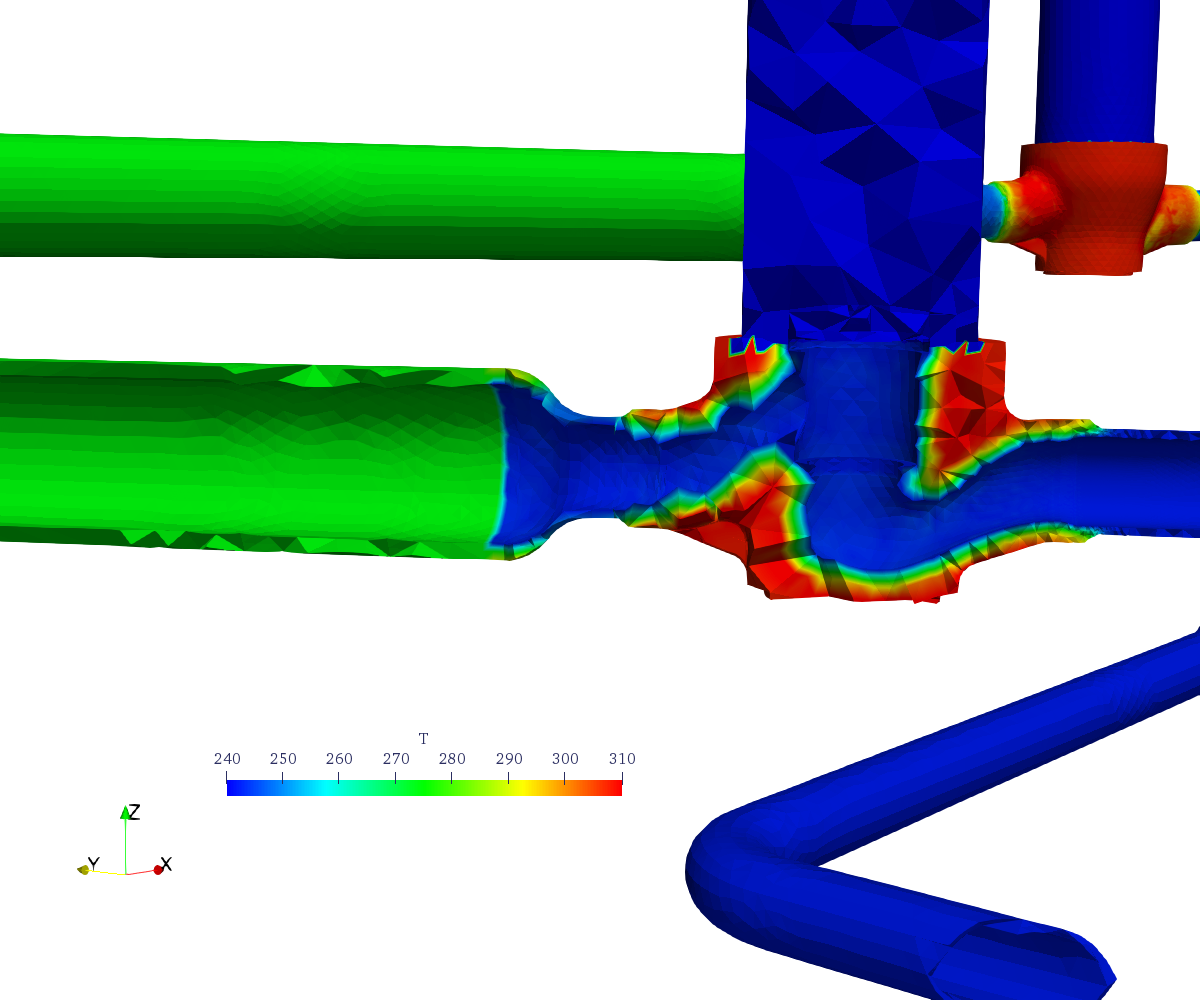
| Remember the main issue of the fatigue analysis in these systems is to analyse what happens around change of piping classes where different materials (i.e. different expansion coefficients) are present, potentially causing high stresses due to differential thermal expansion (or contraction) in transient conditions. Therefore, even though we are dealing with pipes we cannot use beam or circular shell elements, because we need to take into account the three-dimensional effects of the temperature distribution along the pipe thickness. And even if it we could, there are some tees that connect pipes with different nominal diameters that have a non-trivial geometry, such as the weldolet-type junction shown in\ [@fig:weldolet-cad1;@fig:weldolet-mesh2]. | |||
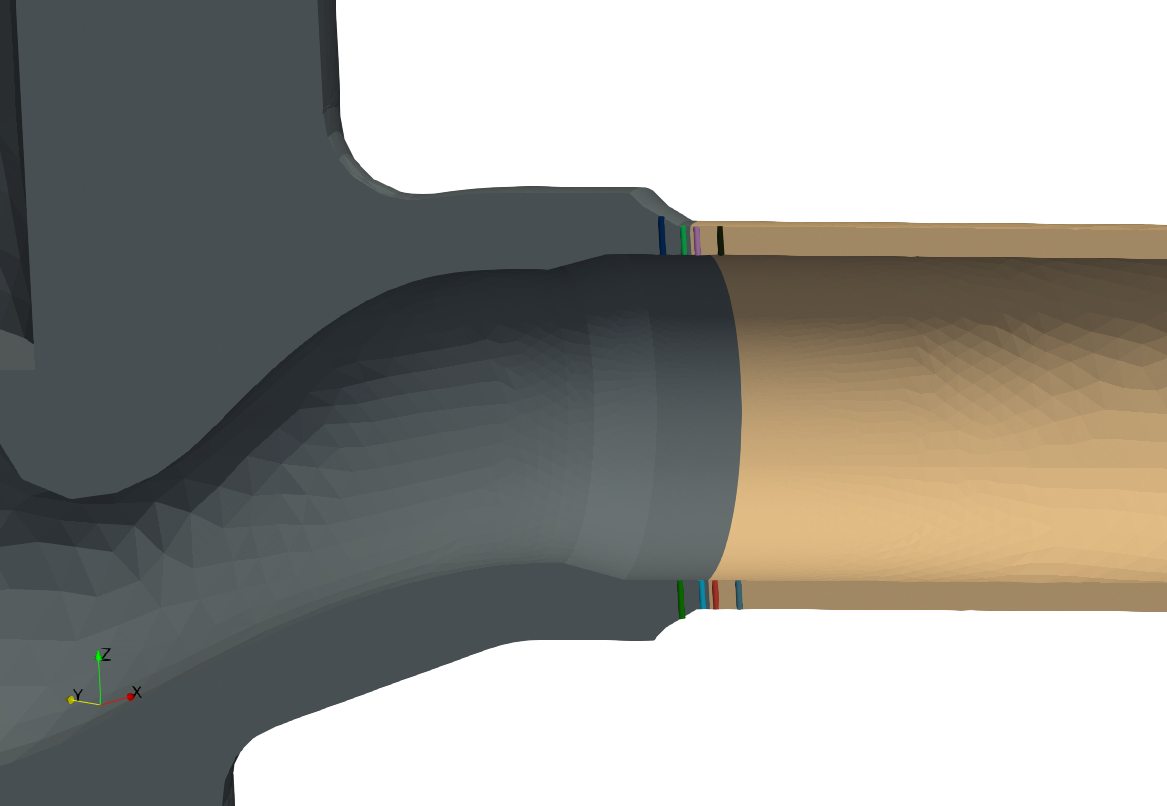
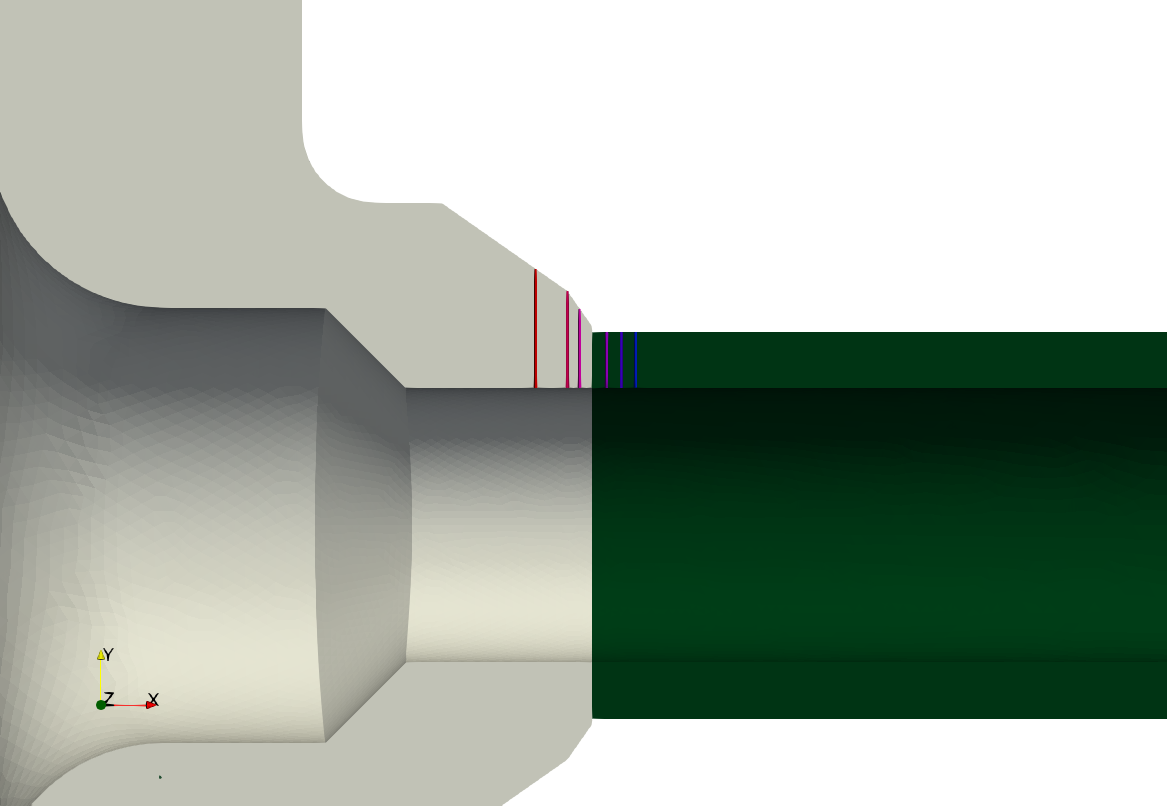
| Remember the main issue of the fatigue analysis in these systems is to analyse what happens around the location of changes of piping classes where different materials (i.e. different expansion coefficients) are present, potentially causing high stresses due to differential thermal expansion (or contraction) under transient conditions. Therefore, even though we are dealing with pipes we cannot use beam or circular shell elements, because we need to take into account the three-dimensional effects of the temperature distribution along the pipe thickness. And even if it we could, there are some tees that connect pipes with different nominal diameters that have a non-trivial geometry, such as the weldolet-type junction shown in\ [@fig:weldolet-cad;@fig:weldolet-mesh]. In this case, there are a number of SCLs (Stress Classification Lines) that go through the pipe’s thickness at both sides of the material interface as illustrated in\ [@fig:weldolet-scls]. It is in these locations that fatigue is to be evaluated. | |||
| dnl 33410 07-3-4D-29 | |||
| {#fig:weldolet-cad1} | |||
| ::::: {#fig:weldolet-cad} | |||
| {#fig:weldolet-cad1} | |||
| {#fig:weldolet-cad2} | |||
| {#fig:weldolet-mesh1} | |||
| CAD model of a piping system with a 3/4-inch weldolet-type fork (stainless steel) from a main 12-inch pipe (carbon steel). | |||
| ::::: | |||
| ::::: {#fig:weldolet-mesh} | |||
| {#fig:weldolet-mesh1} | |||
| {#fig:weldolet-mesh2} | |||
| Three-dimensional unstructured tetrahedra-based grid for the system shown in\ [@fig:weldolet-cad] | |||
| ::::: | |||
| {#fig:weldolet-scls} | |||
| On the one hand, a reasonable number of nodes (remember it is the number of nodes that defines the problem size, not the number of elements) in order to get a decent grid is around 200k for each system. On the other hand, solving a couple of dozens of transient heat transfer problems (which we cannot avoid due to the large thermal inertia of the pipes) during a couple of thousands of seconds over a couple hundred of thousands of nodes might take more time and storage space to hold the results than we might expect. | |||
| There is a wonderful essay by [Isaac Asimov](https://en.wikipedia.org/wiki/Isaac_Asimov) called [“The Relativity of Wrong”](https://en.wikipedia.org/wiki/The_Relativity_of_Wrong) where he introduces the idea that even if something cannot be computed exactly, there are different levels of error. For instance, believing that the Earth is a sphere is less wrong than believing that the Earth is flat, but wrong nonetheless, since it really deviates from a perfect sphere and resembles more an oblate spheroid. | |||
| We can then merge this idea by Asimovve with an adapted version of the [Saint-Venant's principle](https://en.wikipedia.org/wiki/Saint-Venant%27s_principle) and note that the detailed transient temperature distribution is important only around the location of the SCLs. We can then make an engineering approximation and | |||
| 1. compute the transient thermal problem using a reduced mesh around the SCLs, and | |||
| 2. assume the part of the full system which is not contained in the reduced mesh is at an uniform (though not constant) temperature equal to the average of the inner and outer temperatures at each side of the reduced mesh. | |||
| dnl 33300 02-D-3-4 | |||
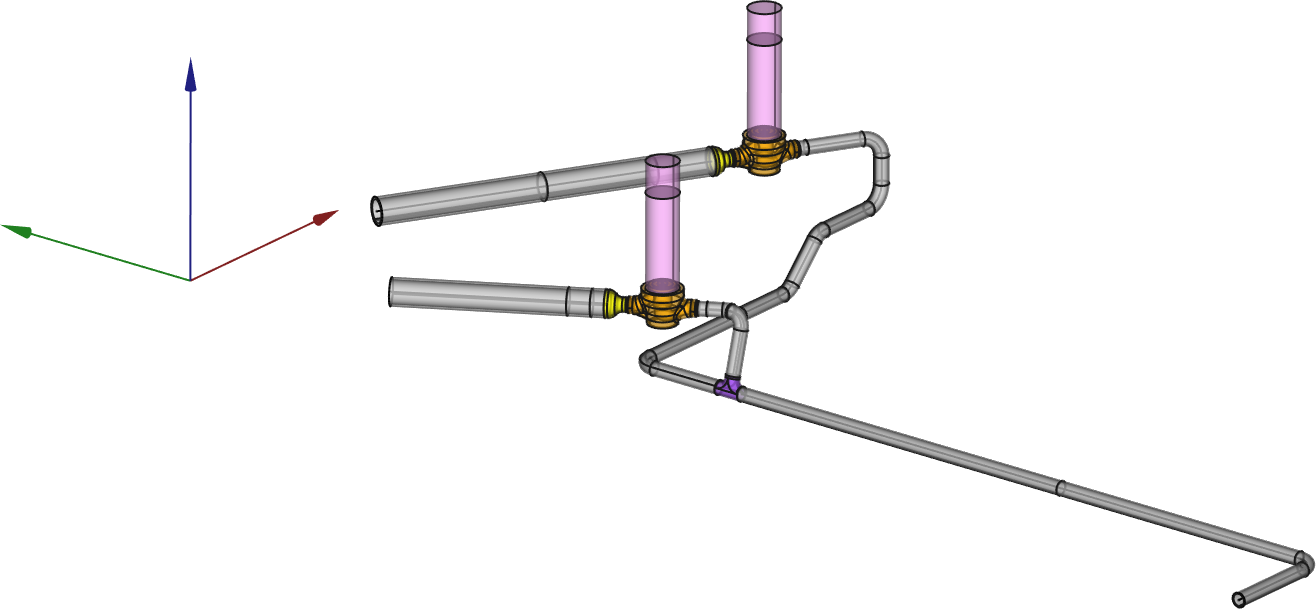
| ::::: {#fig:valve} | |||
| {#fig:valve-cad1} | |||
| {#fig:valve-mesh1} | |||
| {#fig:valve-scls1} | |||
| An example case where the SCLs are located around the junction with the stainless-steel valves and the carbon steel pipe. | |||
| ::::: | |||
| As an example, let us consider the system depicted in\ [@fig:valve-cad1;fig:valve-scls1] where there is a stainless-carbon steel interface at the discharge of the valves. Instead of solving the transient heat-conduction problem with the internal temperature of the pipes equal to the temperature of the water in the reference transient condition of the power plant and an external condition of natural convection to the ambient temperature in the whole mesh of\ [@fig:valve-mesh1], a reduced model consisting of half of one of the two valves and a small length of the pipes at both the valve inlet and outlet is used. Once the temperature distribution\ $\hat{T}(\vec{x},t)$ for each time is obtained in the reduced mesh ([@fig:valve-temp], which has the origin at the center of the valve), the actual temperature distribution\ $T(\vec{x},t)$ is computed by an algebraic genearalisation of $\hat{T}(\vec{x},t)$ in the full coordinate system (where the origin is shown in\ [@fig:valve-cad1]). As stated above, those locations which are not covered by the reduced model are generalised with a time-dependent uniform temperature which is the average of the inner and outer temperatures at the inlet and outlet of the reduced mesh. The result is illustrated in figure\ [@fig:valve-gen]. | |||
| ## The infinite pipe revisited after college | |||
| ::::: {#fig:valve-temp-gen} | |||
| {#fig:valve-temp} | |||
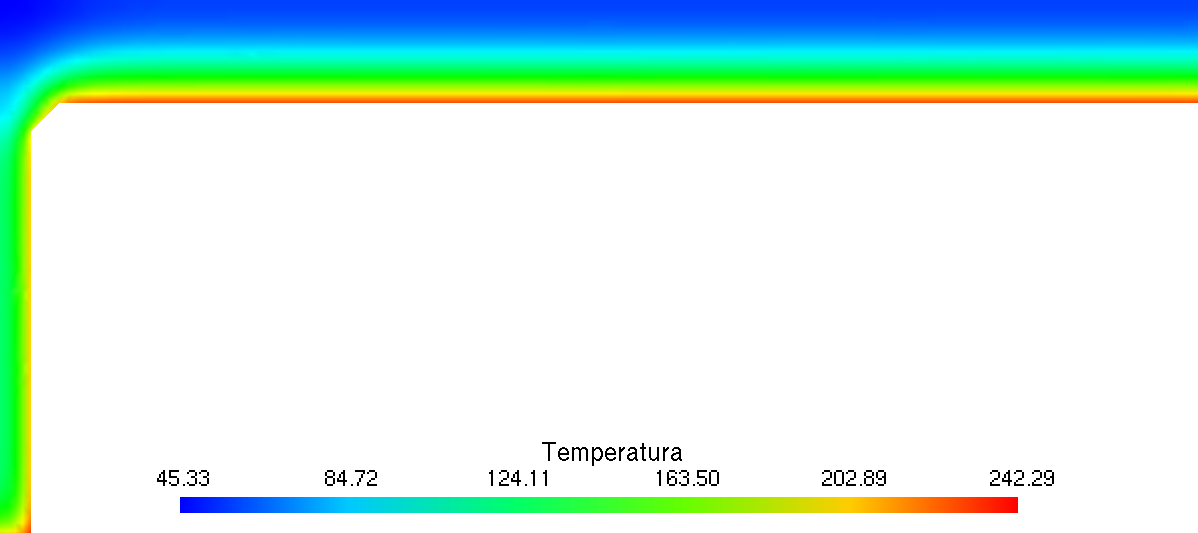
| ![Generalization of the resulting temperature to the original mesh from figure [@fig:valve-mesh1]](valve-gen.png){#fig:valve-gen} | |||
| Computation of the thermal problem in a reduced mesh and generalisation of the result to the full original 3D mesh of figure\ [@fig:valve-mesh1]. | |||
| ::::: | |||
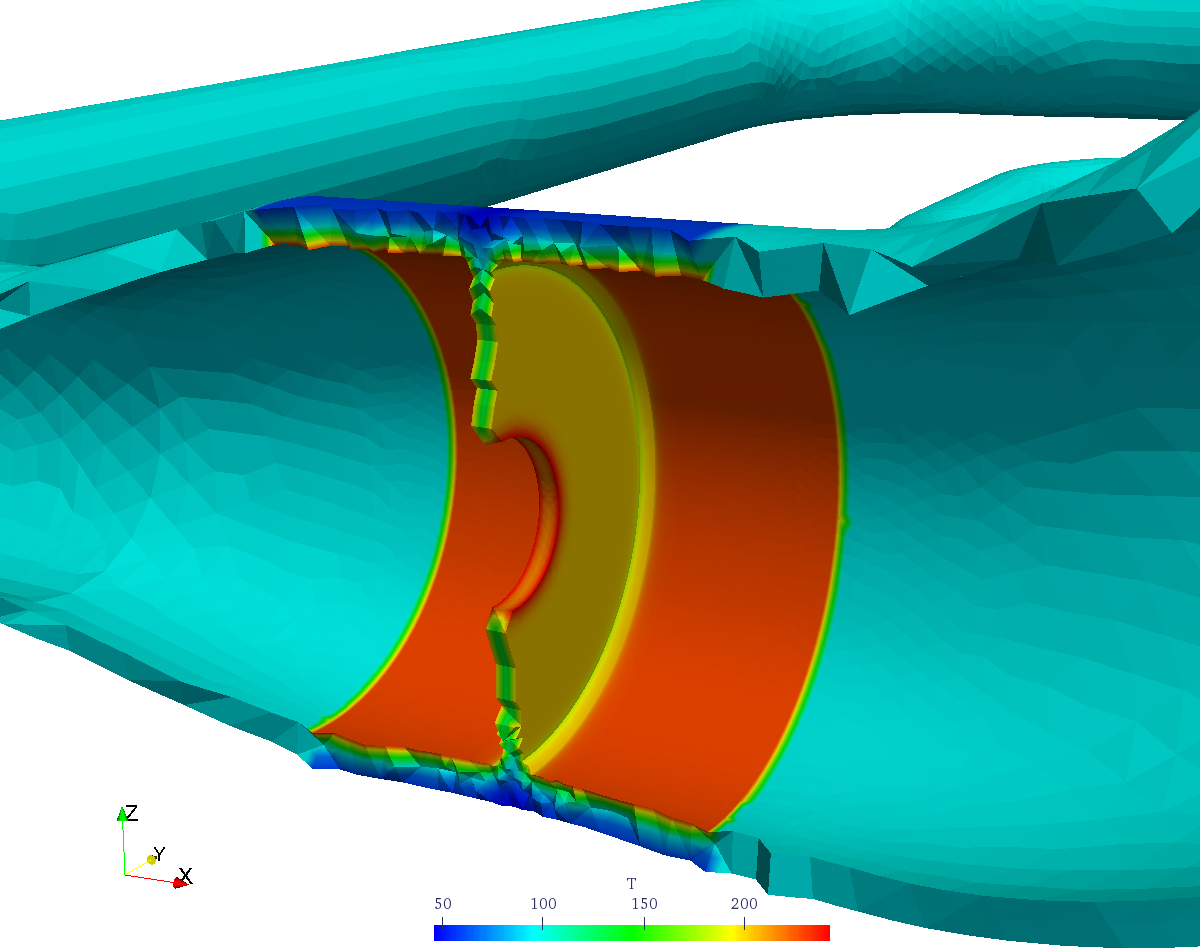
| Please note that there is no need to have a one-to-one correspondence between the elements from the reduced mesh with the elements from the original one. Actually, the reduced mesh contains first-order elements whilst the former has quadratic tetrahedra. Also the grid density is different. Nevertheless, the finite-element solver [Fino](https://www.seamplex.com/fino) used both to solve the heat and the mechanical problems, allows to read functions of space and time defined over one mesh and continuously evaluate and use them into another one even if the two grids have different elements, orders or even dimensions. In effect, in the system from figure [@fig:real-life] the material interface is between a orifice plate made in stainless steel that is welded to a carbon-steel pipe ([@fig:real-mesh2]). The thermal problem can be modeled using a two-dimensional axisymmetric grid [@fig:real-temp] and then generalized to the full three-dimensional mesh using the algebraic manipulation capabilities provided by [Fino](https://www.seamplex.com/fino) (actually by [wasora](https://www.seamplex.com/wasora)) as shown in\ [@fig:real-gen]. | |||
| dnl 33410 10-12D-24 | |||
| ::::: {#fig:real} | |||
| {#fig:real-mesh2} | |||
| {#fig:real-temp} | |||
| {#fig:real-gen} | |||
| The material interface in the system from [@fig:real-life] is configured by an orifice plate made of stainless steel welded to a carbon-steel pipe. | |||
| ::::: | |||
| ## Seismic loads | |||
| ### Natural frequencies | |||
| ### Earthquake spectra | |||
| # The infinite pipe revisited after college | |||
| 3D full | |||
| @@ -366,11 +445,6 @@ struct vs unstruct | |||
| complete vs incomplete (hexa) | |||
| ## The relativity of wrong | |||
| citar a asimov y al report de convergencia | |||
| errors and uncertainties: model parameters (is E what we think? is the material linear?), geometry (does the CAD represent the reality?) equations (any effect we did not have take account), discretization (how well does the mesh describe the geometry?) | |||
| ## Linearity of displacements and stresses | |||
| @@ -384,12 +458,12 @@ cantilever beam, principal stresses, linearity of von mises | |||
| ## Two (or more) materials | |||
| ### Young and Poisson | |||
| / | |||
| two cubes | |||
| ## A parametric tee | |||
| ## Temperature | |||
| ## Bake, break and shake | |||
| # Fatigue | |||
| @@ -408,3 +482,7 @@ Back in College, we all learned how to solve engineering problems. But there is | |||
| * keep in mind there are other methods beside finite elements | |||
| * within the finite element method, there is a wide variety of complexity in the problems that can be solved | |||
| * follow the “five whys rule” before compute anything, probably you do not need to | |||
| * use engineering judgment and make sure understand the [“wronger than wrong”](https://en.wikipedia.org/wiki/Wronger_than_wrong) concept | |||
| dnl errors and uncertainties: model parameters (is E what we think? is the material linear?), geometry (does the CAD represent the reality?) equations (any effect we did not have take account), discretization (how well does the mesh describe the geometry?) | |||
BIN
real-gen.png
View File
BIN
real-mesh2.png
View File
BIN
real-temp.png
View File
BIN
valve-cad1.png
View File
BIN
valve-gen.png
View File
BIN
valve-mesh1.png
View File
BIN
valve-scls1.png
View File
BIN
valve-temp.png
View File
BIN
weldolet-scls.png
View File
Loading…